Trong mặt phẳng tọa độ Oxy cho Hypebol (H):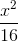 
- 
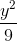= 1. Viết phương trình chính tắc của elip (E) có tiêu điểm trùng với tiêu điểm của (H) và ngoại tiếp hình chữ nhật cơ sở của (H).
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng tọa độ Oxy cho Hypebol (H): - = 1. Viết phương trình chính - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d1: x – y - 2 = 0; d2: x + 2y - 2 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình thoi ABCD có phương trình đường thẳng AC là - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho đường tròn (C): (x – 1)2 + (y + 1)2 = 16, tâm I và điểm A(1 - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho tam giác ABC, có điểm A(2; 3), trọng tâm G(2;0). Hai đỉnh - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho điểm P(-7; 8) và hai đường thẳng d1: 2x + 5y + 3 - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho đường thẳng ∆: x + 2y - 3 = 0; điểm A(1; 0), B(3; -4). Hãy - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có trực tâm là H(3; ), tâm đường tròn ngoại - Luyện Tập 365]
-
[Cho hình thang vuông ABCD vuông tại A và D có đáy lớn là CD, đường thẳng AD có phương trình - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho điểm M(1; 3). Viết phương trình đường thẳng d đi qua M và cắt các - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD biết M(2; 1); N(4; -2); P(2; 0); - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho ∆ABC biết B(2; -1), đường cao qua đỉnh A có phương - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục Oxy, cho đường tròn (C): x2 + y2 = 16. Viết phương trình - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho đường tròn (C): x2 + y2 = và Parabol (P): y2 = x. Tìm - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + y2 - 4x - 4y + 4 = 0 và đường - Luyện Tập 365]
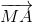+ 3
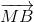| nhỏ nhất.
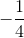), tâm đường tròn ngoại tiếp là K(0; 
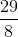), trung điểm cạnh BC là M(
; 3). Xác định tọa độ các đỉnh A, B, C; biết hoành độ của B lớn hơn hoành độ của C.
biết elip cắt đường tròn (C) tại 4 điểm A, B, C, D sao cho AB song song với trục Ox và AB = 2BC.
và Parabol (P): y2 = x. Tìm trên (P) các điểm M mà từ đó kẻ được hai tiếp tuyến tới đường trỏn (C) và hai tiếp tuyến này tạo với nhau một góc bằng 600.