Trong mặt phẳng với hệ tọa độ Oxy cho hình vuông ABCD có M là trung điểm cạnh BC, phương trình đường thẳng MD: x – y – 2 = 0 và C(3; -3). Xác định tọa độ các đỉnh A, B, D biết điểm A thuộc đường thẳng d: 3x + y – 2 = 0
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng với hệ tọa độ Oxy cho hình vuông ABCD có M là trung điểm cạnh BC, phương - Luyện Tập 365]
-
[Trong hệ tọa độ Oxy, cho đường thẳng d: y=√3. Gọi (C) là đường tròn cắt d tại 2 điểm B, - Luyện Tập 365]
-
[Trong mặt phẳng với hệ toạ độ Oxy, hãy viết phương trình các cạnh của tam giác ABC biết - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy viết phương trình chính tắc của elip (E) biết 2 đỉnh thuộc trục - Luyện Tập 365]
-
[Trên mặt phẳng tọa độ Oxy cho hai điểm A(-m; 0),B(m; 0),m là số thực dương. Một điểm M chuyển - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho Hypebol (H) có phương trình - = 1 và đường thẳng - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho đường tròn (C) nội tiếp hình vuông ABCD có phương trình (x - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x -1)2 + (y + 1)2 = 25, điểm M(7; 3). Viết - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua M(0; -1). Biết - Luyện Tập 365]
-
[Trong mặt phẳng hệ tọa độ Oxy, cho tam giác ABC có A(1; 3), B(-1; 1), C(3; 0). Lập phương - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, hãy tính diện tích của tam gíac đều ABC nội tiếp elip - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C): (x – 5)2 + y2 = 41. Viết phương trình - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho elip (E). Tìm các điểm A, B thuộc (E) có hoành độ dương - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho (E): + = 1. Tìm tọa độ các điểm A và B thuộc (E) - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho hình thoi có cạnh bằng 5; chiều cao bằng 4,8; hai đường chéo - Luyện Tập 365]

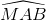 và
và 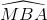 của tam giác MAB có giá trị tuyệt đối luôn bằng
của tam giác MAB có giá trị tuyệt đối luôn bằng 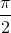 .Tìm quỹ tích điểm M.
.Tìm quỹ tích điểm M.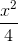 -
- 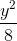 = 1 và đường thẳng d: x - y = 2. Gọi A, B là giao điểm của d và (H). Tìm tọa độ điểm C trên (H) sao cho tam giác ABC có diện tích bằng 8.
= 1 và đường thẳng d: x - y = 2. Gọi A, B là giao điểm của d và (H). Tìm tọa độ điểm C trên (H) sao cho tam giác ABC có diện tích bằng 8.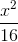 +
+ 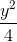 = 1 nhận điểm A(0; 2) làm đỉnh và trục tung làm trục đối xứng .
= 1 nhận điểm A(0; 2) làm đỉnh và trục tung làm trục đối xứng . ; 2) và cắt (C) tại 2 điểm phân biệt A, B sao cho MA = 3MB.
; 2) và cắt (C) tại 2 điểm phân biệt A, B sao cho MA = 3MB.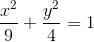 có hoành độ dương sao cho tam giác OAB cân tại O và có diện tích lớn nhất.
có hoành độ dương sao cho tam giác OAB cân tại O và có diện tích lớn nhất.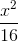 +
+ 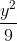 = 1. Tìm tọa độ các điểm A và B thuộc (E) có hoành độ dương sao cho tam giác AOB vuông tại O và có diện tích nhỏ nhất.
= 1. Tìm tọa độ các điểm A và B thuộc (E) có hoành độ dương sao cho tam giác AOB vuông tại O và có diện tích nhỏ nhất.