Trong mặt phẳng với hệ tọa độ Oxy, cho hình thoi ABCD có AC = 2BD và đường tròn tiếp xúc với các cạnh của hình thoi có phương trình x2 + y2 = 4. Viết phương trình chính tắc của elip (E) đi qua các đỉnh A, B, C, D của hình thoi, biết A thuộc Ox.
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình thoi ABCD có AC = 2BD và đường tròn tiếp xúc - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x2 + y2 = 8. Viết phương trình elip - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm cạnh BC, N là - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có diện tích bằng 22, biết rằng - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, lập phương trình chính tắc của Elip (E) biết rằng có - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho hình thoi ABCD tâm I(2;1) và AC = 2BD. Điểm M(0; ) thuộc - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho Elip có phương trình chính tắc: (E): + = - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng d: x - y + 1= 0 và tam giác đều - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục tọa độ Oxy, cho A(1; 2), B(1;-2). Tìm tọa độ điểm C trên đường - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho tam giác cân tại A, A có tọa độ dương, B, C thuộc trục Ox, - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ 2 điểm A, B đối xứng nhau qua trục Ox, C(2; 0), tam giác ABC đều. - Luyện Tập 365]
-
[Trong mặt phẳng toạ độ Oxy, cho tam giác ABC biết có A(1; 1) biết đường thẳng qua trung - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2- 2x - 2y - 8 = 0 và đường thẳng d: 3x - - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho hình thoi ABCD, đường chéo BD nằm trên đường thẳng x - y - 2 = - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (T): x2 + y2 – 4x = 0 và đường thẳng d: - Luyện Tập 365]

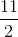 ,
,  ) và đường thẳng AN có phương trình 2x – y – 3 = 0. Tìm tọa độ điểm A.
) và đường thẳng AN có phương trình 2x – y – 3 = 0. Tìm tọa độ điểm A. ) thuộc đường thẳng AB, điểm N(0;7) thuộc đường thẳng CD. Tìm tọa độ đỉnh B biết B có hoành độ dương.
) thuộc đường thẳng AB, điểm N(0;7) thuộc đường thẳng CD. Tìm tọa độ đỉnh B biết B có hoành độ dương.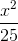 +
+ 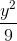 = 1. Viết phương trình đường thẳng song song với Oy và cắt (E) tại hai điểm A, B sao cho AB = 4.
= 1. Viết phương trình đường thẳng song song với Oy và cắt (E) tại hai điểm A, B sao cho AB = 4.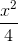 +
+ 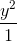 = 1
= 1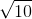 lần bán kính đường tròn (C) và cắt (C) theo dây cung AB = 2√2
lần bán kính đường tròn (C) và cắt (C) theo dây cung AB = 2√2