Trong không gian với hệ tọa độ Oxyz cho tam giác ABC cân tại C có diện tích bằng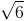 
. Biết A(1;-1;2), B(3;1;0). Tìm tọa độ điểm C biết C thuộc mặt phẳng
(P):x-2y-4z+8=0
DANH SÁCH CÂU HỎI
-
[Trong không gian với hệ tọa độ Oxyz cho tam giác ABC cân tại C có diện t - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng (∆):2x+3y-5=0 và - Luyện Tập 365]
-
[Cho hình chữ nhật ABCD có trung điểm AB là M(4;6). Giao điểm I của hai đ - Luyện Tập 365]
-
[Cho mặt phẳng ( P): 7x + 5y + 2 + 52 = 0 và A(1;-2;5), B(1;4;7). Tìm M t - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với AB = √5, C( -1;- - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho tam giác cân ABC đỉnh A, có trong - Luyện Tập 365]
-
[Trong hệ tọa độ Oxy, cho hình bình hành ABCD có diện tích bằng 4, - Luyện Tập 365]
-
[Trong hệ tọa độ Oxy, cho đường tròn ( C ): x2 + y2 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có đỉnh A(3;5). Phươn - Luyện Tập 365]
-
[Trong mặt phẳng hệ tọa độ Oxy cho đường tròn (C): x2+y2< - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho tam giác ABC vuông cân tại A. Biết rằng cạnh huy - Luyện Tập 365]
-
[Cho elip: 4x2+16y2=64 (E) và điểm M di động trên ( - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy lập phương trình đường tròn có bán kính bé nh - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho đường tròn ( C ): x2 + y2 - Luyện Tập 365]
+
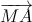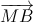| đạt giá trị bé nhất.
; 
), phương trình đường thẳng BC là x – 2y – 4 = 0 và phương trình đường thẳng BG là 7x – 4y – 8 = 0. Tìm tọa độ đỉnh A, B , C. 
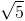. Hãy viết phương trình của (C’)
) thuộc đường thẳng AC, điểm M(2;-3) thuộc đường thẳng AB. Xác định tọa độ các đỉnh của tam giác ABC.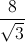
là không đổi. Tính lượng không đổi đó. Tìm M thuộc elip (E) sao cho MF1=2MF2 với F1 là tiêu điểm trái
+ 
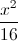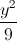= 1 và đường thẳng d: 3x + 4y -12 = 0. Chứng minh rằng đường thẳng d luôn cắt (E ) tại hai điểm phân biệt A,B. Tìm điểm C thuộc (E) sao cho diện tích tam giác ABC bằng 6( đvdt).