Tam giác ABC có phân giác trong (CK): x – 3y – 6 = 0, trung tuyến (BM): x + y – 2 = 0 và trung điểm của BC là N( ; ), tìm phương trình cạnh AC.
DANH SÁCH CÂU HỎI
-
[Tam giác ABC có phân giác trong (CK): x – 3y – 6 = 0, trung tuyến (BM): - Luyện Tập 365]
-
[Tam giác ABC có (AB): 5x + 2y + 7 = 0, (BC): x – 2y – 1 = 0, phân giác t - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn ( C ): x2 + - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có phương trìn - Luyện Tập 365]
-
[Cho elip (E): 4x2+16y2=64. Gọi F1,F - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho hai đường thẳng: (d1):4x-3y-12=0 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình thoi ABCD có tâm I(2;1) và A - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz cho 3 đường thẳng: d1 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho điểm C(2; -5) và đường thẳng ∆ : - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho elip (E) : - Luyện Tập 365]
-
[Trong tọa độ Oxy, cho ∆ABC có A(2;5), B(-4;0), C(5;-1). Viết phương trìn - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có trực tâm H ( - - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M(2;1) và đường thẳng∆ - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho tam giác cân ABC cân ở A có H(2;1) là tru - Luyện Tập 365]

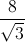 có giá trị không đổi
có giá trị không đổi ) thuộc đường thẳng AB, điểm N(0;7) thuộc đường thẳng CD. Tìm tọa độ đỉnh B biết B có hoành độ dương
) thuộc đường thẳng AB, điểm N(0;7) thuộc đường thẳng CD. Tìm tọa độ đỉnh B biết B có hoành độ dương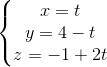 d2:
d2: 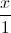 =
=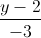 =
=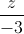 d3:
d3: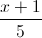 =
=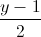 =
=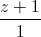
 ) sao cho diện tích tam giác ABC bằng 15.
) sao cho diện tích tam giác ABC bằng 15.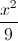 +
+ 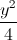 = 1 và hai điểm A(3;-2), B(-3;2). Tìm trên (E) điểm ( C ) có hoành độ và tung độ dương sao cho tam giác ABC có diện tích lớn nhất.
= 1 và hai điểm A(3;-2), B(-3;2). Tìm trên (E) điểm ( C ) có hoành độ và tung độ dương sao cho tam giác ABC có diện tích lớn nhất.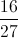 ;
; 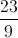 ), phương trình cạnh BC: x – 6y + 4 = 0 và trung điểm cạnh AB là K( -
), phương trình cạnh BC: x – 6y + 4 = 0 và trung điểm cạnh AB là K( - ;
; 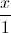 =
=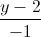 =
=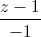 và mặt phẳng (P): ax+by+cz-1=0 (a2+b2 ≠0). Viết phương trình mặt phẳng (P) biết (P) đi qua đường thẳng d và tạo với các trục Oy,Oz các góc bằng nhau
và mặt phẳng (P): ax+by+cz-1=0 (a2+b2 ≠0). Viết phương trình mặt phẳng (P) biết (P) đi qua đường thẳng d và tạo với các trục Oy,Oz các góc bằng nhau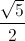 BC và AC:2x-y+2=0. Tìm tọa độ điểm A.
BC và AC:2x-y+2=0. Tìm tọa độ điểm A.