Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có đỉnh C(-4 ; 2), hai đường phân giác trong có phương trình 3x - y + 6 = 0 và x + y - 2 = 0. Tìm tọa độ các đỉnh A và B
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có đỉnh C(-4 ; 2), h - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho hai đường thẳng d1: 2x + y + 5 = 0, - Luyện Tập 365]
-
[Tính diện tích hình phẳng giới hạn bởi parabol (P) : y = 4x – x2 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, xét elip (E) đi qua M(-2 ; -3) và có - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, hãy xác định tọa độ các đỉnh của tam giác ABC vuông - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho điểm E (-1; 0 ) và đường tròn (C - Luyện Tập 365]
-
[Cho tam giác ABC cân tại A, biết phương trình đường thẳng AB, BC lần lượ - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho elip (E) có tiêu điểm thứ nhất là (-√3; 0 ) và đ - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy,cho ba đường thẳng : - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho parabol (P): y2=4x có tiêu đi - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:2x+y+3=0 và elip (E): - Luyện Tập 365]
-
[Trong mặt phẳng Oxy.Viết phương trình đường thẳng tiếp xúc với đường trò - Luyện Tập 365]
-
[Trong mặt phẳng Oxy: Cho hai điểm A(2;1), B(-1;-3) và hai đường thẳn - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho tam giác ABC có trọng tâm G(1;1), đường cao từ đ - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho đường tròn: (C):x2+y - Luyện Tập 365]
; 2) đến (P).
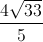). Hãy xác định tọa độ các đỉnh của (E).
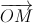+ 4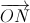
= 
.
= -
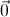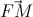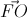; d là đường thẳng bất kì đi qua M, d cắt (P) tại hai điểm phân biệt A,B. Chứng minh rằng tam giác OAB là tam giác vuông
+
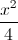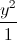=1 Viết PT đường thẳng ∆ vuông góc với d và cắt (E) tại hai điểm A,B sao cho diện tích OAB bằng 1