DANH SÁCH CÂU HỎI

• [Trong hệ tọa độ Đề các vuông góc Oxyz cho hai điểm A(1 ; 1); B(3 ; 3). V - Luyện Tập 365]

  Trong hệ tọa độ Đề các vuông góc Oxyz cho hai điểm A(1 ; 1); B(3 ; 3). Viết phương trình đường tròn đi qua A, B và nhận Ox làm tiếp tuyến

  Chi tiết
• [Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD, biết các đường thẳng AB, - Luyện Tập 365]

  Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD, biết các đường thẳng AB, BC, CD, DA tương ứng đi qua M(10 ; 3), N(7 ; -2), P(-3 ; 4), Q(4 ; -7). Lập phương trình đường thẳng AB.

  Chi tiết
• [Trong mặt phẳng tọa độ Oxy cho elip - Luyện Tập 365]

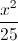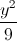  Trong mặt phẳng tọa độ Oxy cho elip  +  = 1 với F₁, F₂ là hai tiêu điểm; M là điểm trên elip sao cho góc F₁MF₂ = 90⁰. Tìm bán kính của đường tròng nội tiếp tam giác MF₁F₂.

  Chi tiết
• [Trong mặt phẳng tọa độ Oxy cho miền phẳng (D) giới hạn bởi cấc đường x = - Luyện Tập 365]

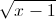  Trong mặt phẳng tọa độ Oxy cho miền phẳng (D) giới hạn bởi cấc đường x = 0; y = 0; y = 10; y = x. Tính thể tích khối tròn xoay được tạo thành khi quay miền (D) xung quanh Ox

  Chi tiết
• [Trong mặt phẳng tọa độ Oxy cho elip (E): - Luyện Tập 365]

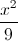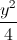  Trong mặt phẳng tọa độ Oxy cho elip (E):  +  = 1 và các điểm A(-3 ; 0) ; I(-1 ; 0). Tìm tọa độ các điểm BC thuộc (E) sao cho I là tâm đường tròn ngoại tiếp tam giác ABC

  Chi tiết
• [Cho tam giác ABC nhọn. Tìm giá trị nhỏ nhất của tổng: T = 2(sinA + sinB - Luyện Tập 365]

  Cho tam giác ABC nhọn. Tìm giá trị nhỏ nhất của tổng: T = 2(sinA + sinB + sinC) + tanA + tanB + tanC.

  Chi tiết
• [Trong mặt phẳng tọa độ Đề - Các Oxy cho hai đường tròn: (I): x2 - Luyện Tập 365]

  Trong mặt phẳng tọa độ Đề - Các Oxy cho hai đường tròn: (I): x² + y² – 4x – 2y + 4 = 0 và (J): x² + y² – 2x – 6y + 6 = 0. Chứng minh: hai đường tròn cắt nhau và viết phương trình các tiếp tuyến chung của chúng.

  Chi tiết
• [Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC với đường cao kẻ từ đ - Luyện Tập 365]

  Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC với đường cao kẻ từ đỉnh B và đường phân giác góc trong của góc A lần lượt có phương trình là x – 2y – 2 = 0 và x – y  - 1 = 0; điểm M(0;2) thuộc đường thẳng AB và AB = 2AC. Tìm tọa độ các đỉnh của tam giác ABC.

  Chi tiết
• [Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có diện tích bằng 2 v - Luyện Tập 365]

  Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có diện tích bằng 2 và đường thẳng AB có phương trình x – y = 0. Biết rằng điểm I(2;1) là trung điểm của đoạn thẳng BC, tìm tọa độ trung điểm K của đoạn thẳng AC.

  Chi tiết
• [Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC cân tại A. Đường thẳn - Luyện Tập 365]

  Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC cân tại A. Đường thẳng AB có phương trình 2x – y + 5 = 0, đường thẳng AC có phương trình 3x – 6y + 1 = 0. Tìm tọa độ trung điểm I của đoạn thẳng BC biết rằng I nằm trên đường thẳng có phương trình 2x – y + 1 = 0.

  Chi tiết
• [Trong mặt phẳng với hệ trục tọa độ vuông góc Oxy, cho đường tròn: x - Luyện Tập 365]

  Trong mặt phẳng với hệ trục tọa độ vuông góc Oxy, cho đường tròn: x² + y² – 6x – 4y + 8 = 0 ( C ) và đường thẳng : 2x – y + 6 = 0 ( d) . Tìm tọa độ điểm M trên ( C ) sao cho khoảng cách từ M đến đường thẳng (d) có giá trị nhỏ nhất.

  Chi tiết
• [Trong mặt phẳng với hệ trục tọa độ vuông góc Oxy, cho tam giác ABC có tr - Luyện Tập 365]

  Trong mặt phẳng với hệ trục tọa độ vuông góc Oxy, cho tam giác ABC có trung điểm của cạnh AB là M(1;4), phương trình đường phân giác trong của góc B là: x – 2y + 2 = 0 (d₁), phương trình đường cao qua C là 3x + 4y – 15 = 0 (d₂). Tìm tọa độ các đỉnh của ∆ABC.

  Chi tiết
• [Trong mặt phẳng tọa độ Oxy cho hình thoi ABCD có hai cạnh AB, CD lần lượ - Luyện Tập 365]

  Trong mặt phẳng tọa độ Oxy cho hình thoi ABCD có hai cạnh AB, CD lần lượt nằm trên 2 đường thẳng d₁: x – 2y + 5 = 0, d₂: x – 2y + 1 = 0. Viết phương trình các đường thẳng AD và BC, biết M(-3 ; 3) thuộc đường thẳng AD và N(-1 ; 4) thuộc đường thẳng BC.

  Chi tiết
• [Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x2 + y - Luyện Tập 365]

  Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x² + y² – 6x – 10y + 9 = 0 và đường thẳng d: x + 2y – 3 = 0. Chứng minh d cắt (C) tại 2 điểm phân biệt A và B. Tìm tọa độ điểm M trên (C) sao cho tam giác MAB cân tại M

  Chi tiết
• [Trong mặt phẳng Oxy, cho đường tròn (C ) : x2 + y2 - Luyện Tập 365]

  Trong mặt phẳng Oxy, cho đường tròn (C ) : x² + y² – 6x + 2y – 15 = 0. Tìm tọa độ điểm M trên đường thẳng d: 3x – 22y – 6 = 0, sao cho từ điểm M kẻ được tới ( C ) hai tiếp tuyến MA, MB (A, B là các tiếp điểm ) mà đường thẳng AB đi qua điểm C(0;1).  

  Chi tiết