Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có điểm M( -  ;
; ) là trung điểm của cạnh AB, điểm H(-2;4) và điểm I(-1;1) lần lượt là chân đường cao kẻ từ B và tâm đường tròn ngoại tiếp tam giác ABC. Tìm tọa độ điểm C.
) là trung điểm của cạnh AB, điểm H(-2;4) và điểm I(-1;1) lần lượt là chân đường cao kẻ từ B và tâm đường tròn ngoại tiếp tam giác ABC. Tìm tọa độ điểm C.
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có điểm M( - - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C ): (x -1)2 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có điểm C thuộ - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng ∆: x – y = 0. Đ - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho các đường thẳng d: x + y – 3 = &n - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A(-3;2) và - Luyện Tập 365]
-
[Tìm phần thực và phần ảo của số phức z = ( - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh B( - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho đường thẳng∆: - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng ∆: x - y - 4 = 0; d: 2x - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho elip (E): - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho đường thẳng∆: x + y + 2 = 0 và đườ - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình chính tắc của elip - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ (Oxy) cho tam giác ABC có phương trình đường cao - Luyện Tập 365]

 ;
; 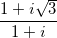 )3
)3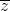 -
- 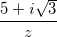 - 1 = 0
- 1 = 0 ; 1). Đường tròn nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB tương ứng tại các điểm D, E, F. Cho D(3 ; 1) và đường thẳng EF có phương trình y - 3 = 0. Tìm tọa độ đỉnh A, biết A có tung độ dương
; 1). Đường tròn nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB tương ứng tại các điểm D, E, F. Cho D(3 ; 1) và đường thẳng EF có phương trình y - 3 = 0. Tìm tọa độ đỉnh A, biết A có tung độ dương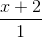 =
= 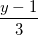 =
= 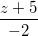 và hai điểm A(-2 ; 1 ; 1); B(-3 ; -1 ; 2). Tìm tọa độ điểm M thuộc đường thẳng ∆ sao cho tam giác MAB có diện tích bằng 3√5
và hai điểm A(-2 ; 1 ; 1); B(-3 ; -1 ; 2). Tìm tọa độ điểm M thuộc đường thẳng ∆ sao cho tam giác MAB có diện tích bằng 3√5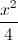 +
+ 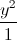 = 1. Tìm tọa độ các điểm A và B thuộc (E), có hoành độ dương sao cho tam giác OAB cân tại O và có diện tích lớn nhất.
= 1. Tìm tọa độ các điểm A và B thuộc (E), có hoành độ dương sao cho tam giác OAB cân tại O và có diện tích lớn nhất.