Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C):(x − 2)2 + (y −1)2 = 5 và đường thẳng d : x−3y −9 = 0. Từ điểm M thuộc d kẻ hai đường thẳng tiếp xúc với (C) lần lượt tại A và B. Tìm tọa độ điểm M sao cho độ dài AB nhỏ nhất.
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C):(x − 2)2 + (y −1)2 = 5 và đường thẳng - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có đỉnh C nằm trên đường thẳng - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có tâm I(3;2). Các đường thẳng AB, - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có trực tâm H(2;2) và tâm đường tròn - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho đường tròn (C) x2 + y2 − x − 9y +18 = 0 và hai điểm A(4;1);B(3;−1). - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho hình chữ nhật ABCD có các đường thẳng AB, AD đi qua M (2;3) - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho tam giác đều ABC nội tiếp đường tròn (C): x2 + y2 – 2x -6y +2 = - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho tam giác ABC có trung điểm cạnh BC là M(-1;0) . Trọng tâm và tâm - Luyện Tập 365]
-
[Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC vuông tại A, phương trình đường cao - Luyện Tập 365]
-
[Trong mặt phẳng với hệ toạ độ Oxy, cho hình bình hành ABCD có tâm I(2;-5) và đường phân - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy , cho tam giác ABC. Phân giác trong góc A, phân giác ngoài góc - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy , cho tam giác ABC cân tại A nội tiếp đường tròn T tâm I( 0;5 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC vuông tại A, phương trình đường cao - Luyện Tập 365]
-
[Trong mặt với hệ trục tọa độ Oxy, cho hình chữ nhật ABCD có AB = 2AD. Gọi N là trung điểm - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục Oxy cho đường tròn (T) (x −1)2 +( y −1)2 =, đường thẳng (d): - Luyện Tập 365]
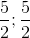) . Viết phương trình đường thẳng AB, biết đỉnh B có tung độ yB >1. 
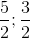) và AC = √26 . 
;
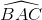có phương trình 2x +y-4 = 0. Biết tam giác ACD có trọng tâm G (-
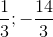). Tìm tọa độ các đỉnh của hình bình hành ABCD.
;1) ,J(2;1) lần lượt là tâm đường tròn ngoại tiếp, nội tiếp tam giác ABC. Tìm tọa độ các điểm A,B,C. 
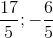)≠ C . Tìm tọa độ các đỉnh A,B,C của tam giác ABC biết xB > 0. 
. 
, đường thẳng (d): mx + y −3 = 0. Tìm m để trên (d) tồn tại duy nhất một điểm M sao cho từ M kẻ được hai tiếp tuyến MA và MB tới (T), (A, B là hai tiếp điểm) thỏa mãn góc giữa hai tiếp tuyến MA và MB bằng 600.