Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình: x-5y-2=0 và đường tròn (C): x2+y2+2x-4y-8=0. Gọi A,B là giao điểm của d với (C) (A có hoành độ dương). Tìm điểm C thuộc đường tròn (C) sao cho AC=2√13?
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình: x-5y-2=0 và đường trò - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có trung điểm cạnh AB là M(-1;2), tâm - Luyện Tập 365]
-
[Trong mặt phẳng toạ độ Oxy cho tam giác ABC có trung tuyến và phân giác trong đỉnh - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC. Các đường thẳng BC, BB’, B’C’ - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD. Các đường thẳng AC và AD - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: 2x – y + 3 = 0. Viết phương t - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C ): x2 + y2 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho các đường tròn (C1): x2 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình thoi ABCD có AC = 2BD và đường tròn tiế - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm của cạn - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C ): x2 + y2 - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho đường tròn (C): x2 + y2 = - Luyện Tập 365]
-
[Cho hình chử nhật ABCD có phương trình đường thẳng AD: 2x+y-1=0, điểm I(-3;2) thuộc - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh A(3; - 7), trực tâm là H(3; - - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho điểm A(0; 2) và ∆ là đường thẳng đi qua O. Gọi H là - Luyện Tập 365]
; 1). Tìm tọa độ các đỉnh của hình chữ nhật ABCD.
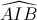= 1200, với I là tâm của (C).
; 
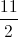) và đường thẳng AN có phương trình 2x – y – 3 = 0. Tìm tọa độ điểm A.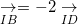
. Tìm toạ độ các đỉnh của hình chử nhật, biết điểm D có hoành độ dương và AD = 2AB.