Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C): x2 + y2+ 2x– 8y –8 = 0. Viết phương trình đường thẳng song song với đường thẳng d: 3x+y-2=0 và cắt đường tròn theo một dây cung có độ dài bằng 6.
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C): x2 + y2 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ toạ độ Oxy cho elip (E): - Luyện Tập 365]
-
[Trong mặt phẳng với hệ toạ độ Oxy cho điểm C(2;-5 ) và đường thẳng ∆: 3x - 4y - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C): (x-1)2 + (y-1) - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho tam giác ABC có - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục toạ độ Oxy, cho tam giác ABC với A(1; -2), đường cao CH - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho đường tròn: x2+y2-2x-4y-20=0(C), có t - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho tam giác ABC có 3 cạnh lần lượt có phương trình là: - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho điểm M(-3;1) và đường tròn (C):x2+y2 - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ với hệ tọa độ Oxy cho tam giác ABC có đỉnh A(-3;4), đường ph - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông cân tại A. Biết cạnh huyền nằm t - Luyện Tập 365]
-
[Cho ∆ABC có tọa độ đỉnh A(2;1). Đường cao từ đỉnh B và trung tuyến từ đỉnh C có phư - Luyện Tập 365]
-
[Viết phương trình đường tròn có tâm thuộc đường thẳng 2x+y-6=0 đi qua M(1;2+√3) và - Luyện Tập 365]
-
[Cho đường tròn (C) có phương trình: X2 + y2 – 2x =0 . Viết ph - Luyện Tập 365]
-
[Cho a,b,c là độ dài 3 cạnh của một tam giác có chu vi bằng 2. Tìm GTNN của biểu thứ - Luyện Tập 365]
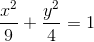và hai điểm A(3;-2), B(-3;2). Tìm trên (E) điểm C có hoành độ và tung độ dương sao cho tam giác ABC có diện tích lớn nhất.
) sao cho diện tích tam giác ABC bằng 15.
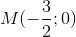là trung điểm của cạnh AB. Đường trung tuyến và đường phân giác trong hạ từ đỉnh A có phương trình lần lượt là 8x - y -3 =0 và x-1=0. Viết phương trình đường thẳng BC.
) thuộc đường thẳng AC, điểm M(2;-3) thuộc đường thẳng AB. Xác định tọa độ các đỉnh của tam giác ABC, biết rằng điểm A có hoành độ âm.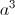
+
+
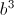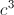) + 15abc