Trong mặt phẳng tọa độ Oxy cho elip (E) có phương trình chính tắc 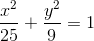 và điểm M(1;1) . Viết phương trình đường thẳng đi qua M và cắt elip tại hai điểm phân biệt A,B sao cho M là trung điểm của AB .
và điểm M(1;1) . Viết phương trình đường thẳng đi qua M và cắt elip tại hai điểm phân biệt A,B sao cho M là trung điểm của AB .
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng tọa độ Oxy cho elip (E) có phương trình chính tắc - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho điểm I(2; 4) và 2 đường thẳng d1: 2x- y -2 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục tọa độ Oxy cho hình thoi ABCD; I(2; 1) là giao điểm của - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho 2 đường tròn (C1): x2 + y2< - Luyện Tập 365]
-
[Trong mặt phẳng hệ tọa độ Oxy, cho hình thoi ABCD có - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy , cho hình chữ nhật ABCD có AD=2AB, gội M, N lần - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC cân tại A có đỉnh A(6;6), đường - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường elip (E): - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn (C): x2 + y2 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang ABCD vuông tại A(1;1) và B. Trên - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):(x-1)2+(y-2)2= - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy , cho hình chữ nhật ABCD có phương trình đường th - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có tâm I(5;3). Tìm tọa độ của điểm - Luyện Tập 365]
-
[Trong mặt phẳng Oxy , cho hai đường thẳng d1: 3x + y - Luyện Tập 365]

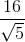
 ) và N(0;7) lần lượt thuộc đường thẳng AB và CD. Tìm tọa độ điểm B biết B có hoành độ dương
) và N(0;7) lần lượt thuộc đường thẳng AB và CD. Tìm tọa độ điểm B biết B có hoành độ dương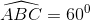 đường tròn (C) có tâm I bán kính 2 tiếp xúc với tất cả các cạnh của hình thoi ( tiếp xúc với AB và CD lần lượt tại M và N, tung độ của I dương). Biết phương trình đường thẳng MN: x+
đường tròn (C) có tâm I bán kính 2 tiếp xúc với tất cả các cạnh của hình thoi ( tiếp xúc với AB và CD lần lượt tại M và N, tung độ của I dương). Biết phương trình đường thẳng MN: x+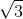 y-1=0, đường thẳng chứa cạnh AD không vuông góc với trục tung và đi qua điểm P(0;3). Viết phương trình các đường thẳng chứa cạnh AB, AD.
y-1=0, đường thẳng chứa cạnh AD không vuông góc với trục tung và đi qua điểm P(0;3). Viết phương trình các đường thẳng chứa cạnh AB, AD.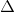 đi qua trung điểm của các cạnh AB và AC có phương trình x+y-4=0. Tìm tọa độ các đỉnh B và C, biết điểm E(1;-3) nằm trên đường cao đi qua đỉnh C của tam giác đã cho.
đi qua trung điểm của các cạnh AB và AC có phương trình x+y-4=0. Tìm tọa độ các đỉnh B và C, biết điểm E(1;-3) nằm trên đường cao đi qua đỉnh C của tam giác đã cho.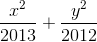 = 1. Gọi F1, F2 là 2 tiêu điểm của (E), M là điểm tùy ý trên (E). Chứng minh rằng MF1.MF2 + OM2 = 4025
= 1. Gọi F1, F2 là 2 tiêu điểm của (E), M là điểm tùy ý trên (E). Chứng minh rằng MF1.MF2 + OM2 = 4025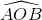 bằng 1200
bằng 1200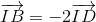 . Tìm tọa độ A, B,C,D biết điểm D có hoành độ dương và AD=2AB
. Tìm tọa độ A, B,C,D biết điểm D có hoành độ dương và AD=2AB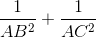 đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất