Trong mặt phẳng toạ độ Oxy, cho hình thoi ABCD có tâm I(3; 3) và đường chéo AC = 2BD. Hai điểm M(2;  ),N(3;
),N(3; 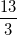 ) lần lượt thuộc AB, CD. Viết phương trình cạnh BD biết điểm B có hoành độ nhỏ hơn 3.
) lần lượt thuộc AB, CD. Viết phương trình cạnh BD biết điểm B có hoành độ nhỏ hơn 3.
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng toạ độ Oxy, cho hình thoi ABCD có tâm I(3; 3) và đường chéo AC = 2B - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d: x - 3y - 1 = 0, d'' - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục tọa độ Oxy , cho điểm A(2;-3), B(3; -2). Tam giác ABC c - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho elip (E): - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (T): (x - 2)2 + (y - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy , cho hình chữ nhật ABCD có tâm I(1; 1) . Các đườ - Luyện Tập 365]
-
[Trong hệ tọa độ Oxy. Viết phương trình đường tròn đi qua điểm A(1; 2) có bán kính b - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục tọa độ Oxy, cho hình thoi ABCD với A(1;0), đường chéo B - Luyện Tập 365]
-
[Trong mặt phẳng Oxy , cho tam giác ABC có phương trình đường phân giác từ đỉnh A: x - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho hình thoi ABCD có A(1; 0), đường chéo BD có phương trình x - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho e líp - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C) (x − 3)2 + (y - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy , cho parabol (P): y2 = 2x và điểm K(2; 0). Đ - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho elip (E): - Luyện Tập 365]

 , trọng tâm G của tam giác ABC nằm trên đường thẳng
, trọng tâm G của tam giác ABC nằm trên đường thẳng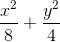 = 1 có các tiêu điểm F1, F2 (F1 có hoành độ âm ). Đường thẳng d đi qua F2 và song song với đường phân giác của góc phần tư thứ nhất cắt (E) tại A và B. Tính diện tích tam giác ABF1
= 1 có các tiêu điểm F1, F2 (F1 có hoành độ âm ). Đường thẳng d đi qua F2 và song song với đường phân giác của góc phần tư thứ nhất cắt (E) tại A và B. Tính diện tích tam giác ABF1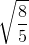
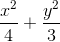 = 1 và đường thẳng ∆:3x + 4y − 12 = 0. Từ điểm M bất kỳ trên ∆ kẻ tới (E) các tiếp tuyến MA, MB. Chứng minh đường thẳng AB luôn đi qua một điểm cố định.
= 1 và đường thẳng ∆:3x + 4y − 12 = 0. Từ điểm M bất kỳ trên ∆ kẻ tới (E) các tiếp tuyến MA, MB. Chứng minh đường thẳng AB luôn đi qua một điểm cố định.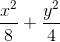 = 1 có các tiêu điểm F1, F2 (F1 có hoành độ âm). Đường thẳng d đi qua F2 và song song với đường phân giác của góc phần tư thứ nhất cắt (E) tại A và B. Tính diện tích tam giác ABF1.
= 1 có các tiêu điểm F1, F2 (F1 có hoành độ âm). Đường thẳng d đi qua F2 và song song với đường phân giác của góc phần tư thứ nhất cắt (E) tại A và B. Tính diện tích tam giác ABF1.