Trong mặt phẳng tọa độ Oxy cho đường tròn (T): x2 + y2 – x - 9y + 18 = 0 và 2 điểm A(4; 1), B(3; -1). Gọi C, D là 2 điểm thuộc (T) sao cho ABCD là một hình bình hành. Viết phương trình đường thẳng CD.
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng tọa độ Oxy cho đường tròn (T): x2 + y2 – x - 9y + 18 = 0 và 2 điểm A(4; - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy cho 2 đường tròn (C1): x2 + y2 - 4y = 0 và (C2): x2 + - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có đỉnh A nằm trên đường thẳng ∆: x - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x2 + y2 - 4x - 4y + 4 =0 và đường - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ (Oxy), cho hình chữ nhật ABCD có phương trình cạnh AB - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d1: 2x + 2y – 1 = - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + y2 – 4x - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy ,cho hình chữ nhật ABCD có: AB = 3√2, BC = 2√2, đ - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, cho hai đường tròn (C1): (x - 1)2 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳ - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho ∆ABC có trọng tâm G( - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục tọa độ vuông góc Oxy, cho hình bình hành ABCD tâm I, bi - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường tròn: (C1): x2&nbs - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD biết M(2; 1); N(4;−2); P(2; - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình thoi MNPQ có M(1; 2), phương trình NQ l - Luyện Tập 365]

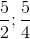 ) nằm trên cạnh AC và thỏa mãn AM = 3MC.
) nằm trên cạnh AC và thỏa mãn AM = 3MC.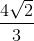 ,điểm I (
,điểm I (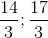 ) thuộc đường thẳng BE. Biết đường thẳng AC có phương trình : x - 5y + 3 = 0 và các điểm A, B có hoành độ nguyên dương. Tìm tọa độ các đỉnh A, B, C, D của hình chữ nhật.
) thuộc đường thẳng BE. Biết đường thẳng AC có phương trình : x - 5y + 3 = 0 và các điểm A, B có hoành độ nguyên dương. Tìm tọa độ các đỉnh A, B, C, D của hình chữ nhật.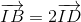 . Tìm tọa độ A, B, C biết điểm D có hoành độ dương và AD=2AB
. Tìm tọa độ A, B, C biết điểm D có hoành độ dương và AD=2AB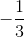 ;
;  ), tâm đường tròn ngoại tiếp tam giác ABC là I(2 ;-1). A ∈ d , x - y + 2 = 0, trung điểm của BC nằm trên d2 : x + y + 3 = 0. Tìm tọa độ A, B, C.
), tâm đường tròn ngoại tiếp tam giác ABC là I(2 ;-1). A ∈ d , x - y + 2 = 0, trung điểm của BC nằm trên d2 : x + y + 3 = 0. Tìm tọa độ A, B, C.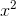 - 2x + 1, điểm I nằm trên cung AB của (P) sao cho tam giác IAB có diện tích lớn nhất. Tìm tọa độ C và D.
- 2x + 1, điểm I nằm trên cung AB của (P) sao cho tam giác IAB có diện tích lớn nhất. Tìm tọa độ C và D.