Trong mặt phẳng xOy cho điểm M(2; 1) và đường thẳng d: x – y + 1 = 0. Viết phương trình đường tròn (C) đi qua M cắt d tại 2 điểm phân biệt sao cho ∆MAB vuông tại M và có diện tích bằng 2.
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng xOy cho điểm M(2; 1) và đường thẳng d: x – y + 1 = 0. Viết phương trình - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho ∆: x – 2y + 5 = 0. Viết phương trình (C) biết (C) tiếp xúc với ∆ - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho ∆ABC có đỉnh C(4; 3) đường phân giác trong và đường trung tuyến - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, gọi H(3;-2), I (8;11), K(4;-1) lần lượt là trực tâm, tâm đường tròn - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho tam giác ABC vuông cân tại A, phương trình đường thẳng BC là 2x - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho tam giác ABC vuông tại A. Gọi M là điểm trên cạnh AC sao - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy cho tam giác ABC cân tại A ( 2;2 ). Đường tròn (C) thay đổi tiếp - Luyện Tập 365]
-
[Câu 5: Trong mặt phẳng Oxy, cho tam giác ABC nội tiếp đường tròn tâm I ( 2; 1) bán kính - Luyện Tập 365]
-
[(1,0 điểm): Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có điểm M là trung điểm - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có đỉnh A(3; 3), tâm đường tròn ngoại - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có phương trình đường thẳng chứa đường - Luyện Tập 365]
-
[Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC cân tại A, phương trình đường trung - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy , cho hình chữ nhật ABCD có A(5;−7) , điểm C thuộc đường - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có điểm C(3;−3) và điểm A thuộc đường - Luyện Tập 365]
-
[Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình chính tắc của elip (E) có tâm sai bằng - Luyện Tập 365]

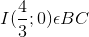 và C có hoành độ dương.
và C có hoành độ dương.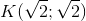 .
.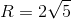
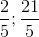 )
)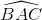 là x − y = 0. Tìm tọa độ các đỉnh B, C biết rằng BC =
là x − y = 0. Tìm tọa độ các đỉnh B, C biết rằng BC = 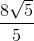 và góc
và góc 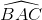 =1350.
=1350. , biết diện tích của tứ giác tạo bởi các tiêu điểm và các đỉnh trên trục bé của (E) bằng 24.
, biết diện tích của tứ giác tạo bởi các tiêu điểm và các đỉnh trên trục bé của (E) bằng 24.