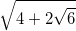Chứng minh rằng với mọi số thực dương x, y, z thoả mãn x(x + y + z) = 3yz, ta có: (x + y)3 + ( x + z)3 + 3(x + y)(x + z)(y + z) ≤ 5(y + z)3
DANH SÁCH CÂU HỎI
-
[Chứng minh rằng với mọi số thực dương x, y, z thoả mãn x(x + y + z) = 3y - Luyện Tập 365]
-
[Cho a, b , c là các số thực dương. Tìm giá trị lớn nhất của biểu thức P - Luyện Tập 365]
-
[Cho x, y là các số thực dương thỏa mãn điều kiện xy ≤y -1. Tìm giá trị l - Luyện Tập 365]
-
[Cho các số thực dương a, b , c thỏa mãn điều kiện (a + c )(b + c) = 4c - Luyện Tập 365]
-
[Cho a và b là các số thực dương thỏa mãn 2(a2 + b2 - Luyện Tập 365]
-
[Cho x , y , z là ba số thực thuộc đoạn [1 ; 4] và x≥ y, x≥ z - Luyện Tập 365]
-
[Xét các số thực không âm a, b ,c thỏa mãn a + b + c = 1. Tìm giá trị lớn - Luyện Tập 365]
-
[Cho các số dương a, b, c thỏa mãn a + b + c = 1. Tìm giá trị nhỏ nhất củ - Luyện Tập 365]
-
[Cho các số thực không âm a, b, c thỏa mãn: a + b + c = 1. Tìm giá trị nh - Luyện Tập 365]
-
[Cho x, y , z là các số thực dương thỏa xyz = 1. Chứng minh: - Luyện Tập 365]
-
[Cho a, b, c là các số dương thỏa mãn: abc = 8. Hãy tìm giá trị lớn nhất - Luyện Tập 365]
-
[Cho các số thực x, y thây đổi nhưng luôn thỏa mãn x + y - 3 = 4( - Luyện Tập 365]
-
[Cho x, y là các số dương thỏa mãn - Luyện Tập 365]
-
[Cho các số thực x , y , z thỏa mãn - Luyện Tập 365]
-
[Cho hai số thực không âm x, y thỏa mãn x2 + y2 + X - Luyện Tập 365]
- 
.
- 
.
+ 
- 
.
+ 
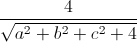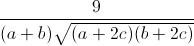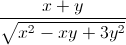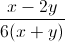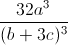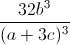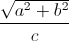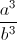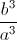) - 9(
+ 
)
+ 
+ 
+ 
+ 
.
+ 
+
≥ 
+ 
+ 
+ 
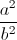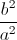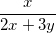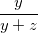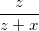
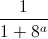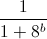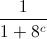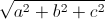
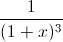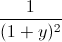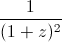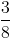
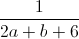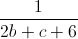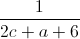
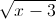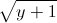) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức M = 
+ 
+ 
+ 
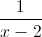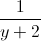
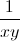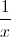= 3. Tìm giá trị lớn nhất của biểu thức : M =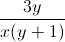 
+ 
+ 
- 
- 
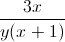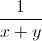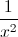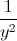
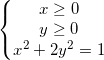Chứng minh rằng 1 + 
≤ 
+ 
≤ 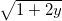