Cho tam giác vuông cân ABC (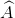 = 900, AB = AC). Trên cạn AC lấy điểm M sao cho MC : MA = 1 : 3. Kẻ đường thẳng vuông góc với AC tại C, cắt tia BM tại K. Kẻ BE ⊥ CK.
a. Chứng minh tứ giác ABEC là hình vuông.
b. Chứng minh
= 900, AB = AC). Trên cạn AC lấy điểm M sao cho MC : MA = 1 : 3. Kẻ đường thẳng vuông góc với AC tại C, cắt tia BM tại K. Kẻ BE ⊥ CK.
a. Chứng minh tứ giác ABEC là hình vuông.
b. Chứng minh 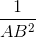 =
= 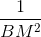 +
+ 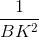 c. Biết BM = 6 cm. Tính các cạnh của tam giác MCK.
c. Biết BM = 6 cm. Tính các cạnh của tam giác MCK.

Câu hỏi
Nhận biếtCho tam giác vuông cân ABC (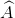 = 900, AB = AC). Trên cạn AC lấy điểm M sao cho MC : MA = 1 : 3. Kẻ đường thẳng vuông góc với AC tại C, cắt tia BM tại K. Kẻ BE ⊥ CK.
= 900, AB = AC). Trên cạn AC lấy điểm M sao cho MC : MA = 1 : 3. Kẻ đường thẳng vuông góc với AC tại C, cắt tia BM tại K. Kẻ BE ⊥ CK.
a. Chứng minh tứ giác ABEC là hình vuông.
b. Chứng minh 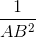 =
= 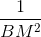 +
+ 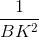
c. Biết BM = 6 cm. Tính các cạnh của tam giác MCK.
 (cm), MK = 2 (cm), KC = 1
(cm), MK = 2 (cm), KC = 1 (cm)
(cm)  (cm), MK = 2 (cm), KC =
(cm), MK = 2 (cm), KC =  (cm)
(cm)  (cm), MK = 2 (cm), KC = 1
(cm), MK = 2 (cm), KC = 1 (cm)
(cm)  (cm), MK = 2 (cm), KC = 1
(cm), MK = 2 (cm), KC = 1 (cm)
(cm) Đáp án đúng: D
Lời giải của Luyện Tập 365
a. Xét tứ giác ABEC có 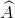 =
= 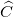 =
= 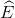 = 900 và AB = AC nên ABEC là hình vuông.
= 900 và AB = AC nên ABEC là hình vuông.
b. Kẻ đường thẳng vuông góc với BM tại B cắt EC tại N. Xét ∆ABM và ∆EBN có: AB = AE (vì ABEC là hình vuông).
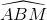 =
= 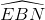 (2 góc nhọn có cạnh tương ứng vuông góc).
(2 góc nhọn có cạnh tương ứng vuông góc).
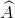 =
= 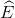 = 900.
= 900.
Vậy ∆ABM = ∆EBN (g.c.g) => BM = BN.
Áp dụng hệ thức lượng vào tam giác vuông BNK ta có:
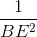 =
= 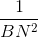 +
+ 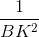 , mà AB = BE và BM = BN.
, mà AB = BE và BM = BN.
Vậy 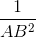 =
= 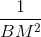 +
+ 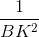
c. MC : MA = 1 : 3 => MA = 3MC và AB = AC = 4MC.
Đặt MC = x thì MA = 3x, AB = 4x
Áp dụng định lý Pytago vào tam giác vuông ABM:
AB2 + AC2 = BM2 => (4x)2 + (3x)2 = 62 ⇔ 25x2 = 36 ⇔ x = 
Vậy MC = 1 (cm); AB = 4x =
(cm); AB = 4x = 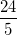 = 4
= 4 (cm).
(cm).
Vì CK // AB nên ∆MCK ∽ ∆MAB => 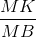 =
= 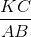 =
= 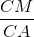 =
=  => MK = 2 (cm) và KC =
=> MK = 2 (cm) và KC = 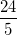 : 3 = 1
: 3 = 1 (cm).
(cm).
a. Xét tứ giác ABEC có 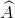 =
= 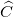 =
= 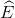 = 900 và AB = AC nên ABEC là hình vuông.
= 900 và AB = AC nên ABEC là hình vuông.
b. Kẻ đường thẳng vuông góc với BM tại B cắt EC tại N. Xét ∆ABM và ∆EBN có: AB = AE (vì ABEC là hình vuông).
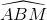 =
= 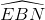 (2 góc nhọn có cạnh tương ứng vuông góc).
(2 góc nhọn có cạnh tương ứng vuông góc).
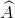 =
= 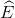 = 900.
= 900.
Vậy ∆ABM = ∆EBN (g.c.g) => BM = BN.
Áp dụng hệ thức lượng vào tam giác vuông BNK ta có:
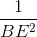 =
= 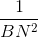 +
+ 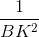 , mà AB = BE và BM = BN.
, mà AB = BE và BM = BN.
Vậy 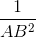 =
= 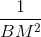 +
+ 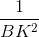
c. MC : MA = 1 : 3 => MA = 3MC và AB = AC = 4MC.
Đặt MC = x thì MA = 3x, AB = 4x
Áp dụng định lý Pytago vào tam giác vuông ABM:
AB2 + AC2 = BM2 => (4x)2 + (3x)2 = 62 ⇔ 25x2 = 36 ⇔ x = 
Vậy MC = 1 (cm); AB = 4x =
(cm); AB = 4x = 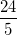 = 4
= 4 (cm).
(cm).
Vì CK // AB nên ∆MCK ∽ ∆MAB => 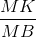 =
= 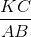 =
= 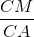 =
=  => MK = 2 (cm) và KC =
=> MK = 2 (cm) và KC = 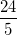 : 3 = 1
: 3 = 1 (cm).
(cm).
Câu hỏi liên quan
-

Trong mặt phẳng với hệ trục Oxy, cho hình thoi ABCD biết phương trình của một đường chéo là 3x+y-7=0, điểm B(0;-3), diện tích hình thoi bằng 20. Tìm tọa độ các đỉnh còn lại của hình thoi.
-

Tính tích phân I =
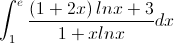
-

Giải phương trình (1-
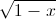 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Giải hệ phương trình
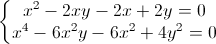 (x, y
(x, y R)
R) -

Tìm số phức z thỏa mãn
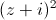 +
+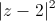 =2
=2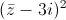 .
. -

Cho hàm số y =
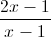 a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất. -

Cho hàm số y =x3-6x2+3mx+2, với m là tham số thực. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi m=3 (HS tự làm). b) Tìm m sao cho đồ thị của hàm số đã cho có các điểm cực trị A,B thỏa mãn AB=4√65.
-

Trong mặt phẳng với hệ trục Oxy, cho hai đường thẳng ∆1: 3x+y+5=0, ∆2: x-2y-3=0 và đường tròn (C):
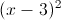 +
+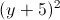 =25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2.
=25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2. -

Giải phương trình
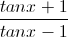 =
=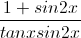
-

Cho các số thực x,y thỏa mãn x
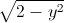 + y
+ y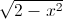 = 2 Tìm giá trị lớn nhất của biểu thức P=
= 2 Tìm giá trị lớn nhất của biểu thức P=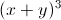 -12(x-1).(y-1)+√xy.
-12(x-1).(y-1)+√xy.
