Trong không gian với hệ tọa độ Oxyz, cho A(0 ; 0; 3), M(1; 2; 0). Viết phương trình mặt phẳng (P) qua A và cắt Ox, Oy lần lượt tại B, C sao cho ∆ABC có trọng tâm thuộc AM.

Câu hỏi
Nhận biếtTrong không gian với hệ tọa độ Oxyz, cho A(0 ; 0; 3), M(1; 2; 0). Viết phương trình mặt phẳng (P) qua A và cắt Ox, Oy lần lượt tại B, C sao cho ∆ABC có trọng tâm thuộc AM.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Từ giả thiết ta giả sử B(b; 0; 0) và C(0; c ; 0), suy ra ∆ABC có trọng tâm G(  ;
; 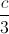 ; 1)
; 1)
Phương trình đường thẳng (AM) được cho bởi: (AM) qua A và có vtcp 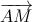 (1; 2; - 3) ⇔ (AM) :
(1; 2; - 3) ⇔ (AM) : 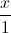 =
= 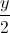 =
= 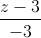
Vì G thuộc (AM) nên :  =
= 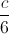 =
= 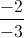 =>
=> 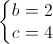 =>
=> 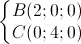
Từ đó, bằng việc sử dụng phương trình mặt phẳng chắn ta được :
(P): 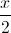 +
+ 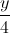 +
+ 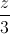 = 1 ⇔ (P): 6x + 3y + 4z – 12 = 0.
= 1 ⇔ (P): 6x + 3y + 4z – 12 = 0.
Từ giả thiết ta giả sử B(b; 0; 0) và C(0; c ; 0), suy ra ∆ABC có trọng tâm G(  ;
; 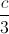 ; 1)
; 1)
Phương trình đường thẳng (AM) được cho bởi: (AM) qua A và có vtcp 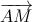 (1; 2; - 3) ⇔ (AM) :
(1; 2; - 3) ⇔ (AM) : 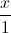 =
= 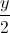 =
= 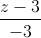
Vì G thuộc (AM) nên :  =
= 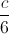 =
= 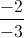 =>
=> 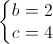 =>
=> 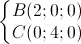
Từ đó, bằng việc sử dụng phương trình mặt phẳng chắn ta được :
(P): 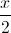 +
+ 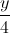 +
+ 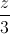 = 1 ⇔ (P): 6x + 3y + 4z – 12 = 0.
= 1 ⇔ (P): 6x + 3y + 4z – 12 = 0.
Câu hỏi liên quan
-

Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC cân, cạnh đáy BC có phương trình x + y + 1 = 0. Phương trình đường cao vẽ từ B là x - 2y - 2 = 0. Điểm M(2; 1) thuộc đường cao vẽ từ C. Viết phương trình các cạnh bên của tam giác ABC.
-

Tìm số phức z thỏa mãn
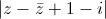 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 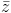 ) là số ảo.
) là số ảo. -

Tính tích phân I=
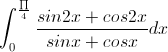
-

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): 2x - y + z - 2 = 0, (β): x + 2y +2z - 4 = 0. Viết phương trình đường thẳng d nằm trong (α), song song với (β) và cách (β) một khoảng bằng 1.
-

Giải phương trình
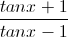 =
=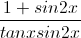
-

Trong mặt phẳng với hệ trục Oxy, cho hình thoi ABCD biết phương trình của một đường chéo là 3x+y-7=0, điểm B(0;-3), diện tích hình thoi bằng 20. Tìm tọa độ các đỉnh còn lại của hình thoi.
-

Cho hàm số y =x3-6x2+3mx+2, với m là tham số thực. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi m=3 (HS tự làm). b) Tìm m sao cho đồ thị của hàm số đã cho có các điểm cực trị A,B thỏa mãn AB=4√65.
-

Tìm số phức z thỏa mãn
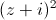 +
+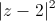 =2
=2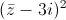 .
. -

Giải phương trình:
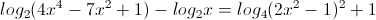
-

Cho hàm số y =
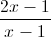 a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng d : y = 3x+m cắt đồ thị (C) tại hai điểm A, B sao cho độ dài AB nhỏ nhất.
