Quả cầu của con lắc lò xo dao động điều hòa theo phương trình x = 4cos(πt - π/2)cm. Quãng đường quả cầu đi được trong 2,25s đầu tiên là:

Câu hỏi
Nhận biếtQuả cầu của con lắc lò xo dao động điều hòa theo phương trình x = 4cos(πt - π/2)cm. Quãng đường quả cầu đi được trong 2,25s đầu tiên là:
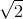 cm
cm 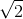 cm
cm Đáp án đúng: C
Phương pháp giải
Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn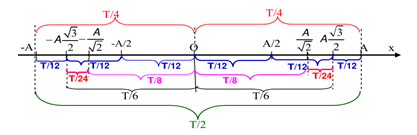
Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn
Lời giải của Luyện Tập 365
Ta có: 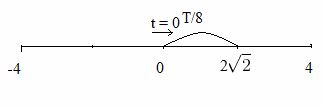
t = 0 =>
$$\left\{ \matrix{ x = 0 \hfill \cr v > 0 \hfill \cr} \right.$$
T = 2π/ω = 2 (s)
$$t = 2,25{\rm{s}} \to {t \over T} = {9 \over 8} \to t = {9 \over 8}T = T + {T \over 8}$$
Theo hình vẽ :
$$s = 4A + {{A\sqrt 2 } \over 2} = 4.4 + 2\sqrt 2 = 16 + 2\sqrt 2 cm$$
Ta có: 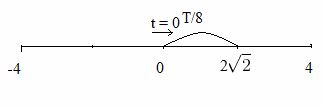
t = 0 =>
$$\left\{ \matrix{ x = 0 \hfill \cr v > 0 \hfill \cr} \right.$$
T = 2π/ω = 2 (s)
$$t = 2,25{\rm{s}} \to {t \over T} = {9 \over 8} \to t = {9 \over 8}T = T + {T \over 8}$$
Theo hình vẽ :
$$s = 4A + {{A\sqrt 2 } \over 2} = 4.4 + 2\sqrt 2 = 16 + 2\sqrt 2 cm$$
Câu hỏi liên quan
-

Nguyên nhân sâu xa của hiện tượng tán sắc ánh sáng là sự phụ thuộc của chiết suất môi trường vào:
-

Dao động cơ học là
-

Câu nào dưới đây không đúng với vật dao động điều hòa có phương trình x = Acos(
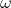 t +
t + 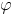 )
) -

Dao động của một vật có phương trình: x = acosωt + asinωt. Biên độ dao động của vật là
-

Ánh sáng trắng là ánh sáng:
-

Câu phát biểu nào sau đây về hiện tượng tán sắc là sai ?
-

Phát biểu nào sau đây là không đúng? Gia tốc của một vật dao động điều hòa
-

Một chùm sáng trắng song song đi từ không khí vào thủy tinh, với góc tới lớn hơn không, sẽ
-

Chùm tia ló ra khỏi lăng kính trong một máy quang phổ, trước khi đi qua thấu kính của buồng ảnh là:
-

Một chất điểm dao động điều hòa trên trục Ox với chu kỳ T. Vị trí cân bằng của chất điểm trùng với gốc tọa độ, khoảng thời gian ngắn nhất để nó đi từ vị trí có li độ x = A đến vị trí có li độ x =
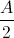 là
là
