Một vật dao động điều hòa với biên độ A. Tìm quãng đường nhỏ nhất vật đi được trong khoảng thời gian 2T/3.

Câu hỏi
Nhận biếtMột vật dao động điều hòa với biên độ A. Tìm quãng đường nhỏ nhất vật đi được trong khoảng thời gian 2T/3.
Đáp án đúng: D
Phương pháp giải
Ứng dụng đường tròn lượng giác, công thức $$\Delta t = {\alpha \over \omega } = {{\alpha T} \over {2\pi }}$$ , và áp dụng công thức tính quãng đường nhỏ nhất: $${S_{{\rm{min}}}} = 2{\rm{A(1 - cos}}{{\Delta \varphi } \over 2})$$
Ứng dụng đường tròn lượng giác, công thức $$\Delta t = {\alpha \over \omega } = {{\alpha T} \over {2\pi }}$$ , và áp dụng công thức tính quãng đường nhỏ nhất: $${S_{{\rm{min}}}} = 2{\rm{A(1 - cos}}{{\Delta \varphi } \over 2})$$
Lời giải của Luyện Tập 365
Hình vẽ :
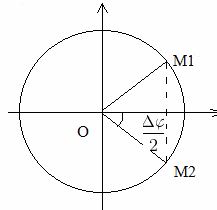
Có $$\Delta t = {{2T} \over 3} \to \Delta \varphi = \Delta t.\omega = {{2T} \over 3}{{2\pi } \over T} = {{4\pi } \over 3} = \pi + {\pi \over 3}$$
$${S_{\min }} = {S_{(\pi )}} + {S_{({\pi \over 3})}} = 2A + 2A(1 - c{\rm{os}}{{{\pi \over 3}} \over 2}) = 4A - A\sqrt 3 $$
Hình vẽ :

Có $$\Delta t = {{2T} \over 3} \to \Delta \varphi = \Delta t.\omega = {{2T} \over 3}{{2\pi } \over T} = {{4\pi } \over 3} = \pi + {\pi \over 3}$$
$${S_{\min }} = {S_{(\pi )}} + {S_{({\pi \over 3})}} = 2A + 2A(1 - c{\rm{os}}{{{\pi \over 3}} \over 2}) = 4A - A\sqrt 3 $$
Câu hỏi liên quan
-

Chuyển động nào sau đây của chất điểm là một dao động điều hòa?
-

Khoảng thời gian ngắn nhất mà trạng thái một vật dao động tuần hoàn lặp lại như cũ gọi là
-

Chọn câu đúng
-

Một vật nhỏ dao động điều hòa theo một trục cố định. Phát biểu nào sau đây đúng?
-

Ánh sáng có tần số lớn nhất trong số các ánh sáng đơn sắc: đỏ, lam, chàm, tím là ánh sáng:
-

Tại sao khi chùm tia sáng mặt trời đi qua một tấm thủy tinh phẳng lại không thấy bị tán sắc thành những màu cơ bản?
-

Ánh sáng đơn sắc là ánh sáng:
-

Khi chiếu ánh sáng trắng vào một lăng kính thì tia sáng nào bị lệch về phía đáy nhiều nhất ?
-

Dao động điều hòa là
-

Một chất điểm dao động điều hòa trên trục Ox với chu kỳ T. Vị trí cân bằng của chất điểm trùng với gốc tọa độ, khoảng thời gian ngắn nhất để nó đi từ vị trí có li độ x = A đến vị trí có li độ x =
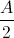 là
là
