Hạt nhân \({}_{84}^{210}Po\) đứng yên, phân rã α biến thành hạt nhân X: \({}_{84}^{210}Po \to {}_2^4He + {}_Z^AX\). Biết khối lượng của các nguyên tử tương ứng là mPo= 209,982876u, mHe = 4,002603u, mX = 205,974468u. Biết 1u = 931,5MeV/c2. Vận tốc của hạt α bay ra xấp xỉ bằng

Câu hỏi
Nhận biếtHạt nhân \({}_{84}^{210}Po\) đứng yên, phân rã α biến thành hạt nhân X: \({}_{84}^{210}Po \to {}_2^4He + {}_Z^AX\). Biết khối lượng của các nguyên tử tương ứng là mPo= 209,982876u, mHe = 4,002603u, mX = 205,974468u. Biết 1u = 931,5MeV/c2. Vận tốc của hạt α bay ra xấp xỉ bằng
Đáp án đúng: D
Phương pháp giải
Năng lượng toả ra của phản ứng: ∆E = (mt – ms)c2 = Ks – Kt
(mt, Kt và ms, Ks lần lượt là tổng khối lượng và tổng động năng của các hạt trước và sau phản ứng)
Áp dụng định luật bảo toàn động lượng
Công thức liên hệ giữa động năng và động lượng: p2 = 2mK
Công thức động năng: K = mv2/2
Năng lượng toả ra của phản ứng: ∆E = (mt – ms)c2 = Ks – Kt
(mt, Kt và ms, Ks lần lượt là tổng khối lượng và tổng động năng của các hạt trước và sau phản ứng)
Áp dụng định luật bảo toàn động lượng
Công thức liên hệ giữa động năng và động lượng: p2 = 2mK
Công thức động năng: K = mv2/2
Lời giải của Luyện Tập 365
Phương trình phản ứng: \({}_{84}^{210}Po \to {}_2^4He + {}_Z^AX\)
Năng lượng toả ra của phản ứng: ∆E = (mPo – mHe – mX)c2 = 5,407 MeV = KHe + KX
Áp dụng định luật bảo toàn động lượng:
\(\overrightarrow {{p_{He}}} + \overrightarrow {{p_X}} = 0 \Rightarrow {p_{He}} = {p_X} \Leftrightarrow {m_{He}}{K_{He}} = {m_X}{K_X} \Rightarrow {K_X} = {{4,002603} \over {205,974468}}{K_{He}} = 0,0194{K_{He}}\)
=> ∆E = 5,407 MeV = KHe + KX = KHe + 0,0194KHe => KHe = 5,304 MeV
\( \Rightarrow {v_{He}} = \sqrt {{{2{K_{He}}} \over {{m_{He}}}}} = \sqrt {{{{{2.5,304.1,6.10}^{ - 13}}} \over {{{4,002603.1,66055.10}^{27}}}}} = {16.10^6}m/s\)
Chọn D
Phương trình phản ứng: \({}_{84}^{210}Po \to {}_2^4He + {}_Z^AX\)
Năng lượng toả ra của phản ứng: ∆E = (mPo – mHe – mX)c2 = 5,407 MeV = KHe + KX
Áp dụng định luật bảo toàn động lượng:
\(\overrightarrow {{p_{He}}} + \overrightarrow {{p_X}} = 0 \Rightarrow {p_{He}} = {p_X} \Leftrightarrow {m_{He}}{K_{He}} = {m_X}{K_X} \Rightarrow {K_X} = {{4,002603} \over {205,974468}}{K_{He}} = 0,0194{K_{He}}\)
=> ∆E = 5,407 MeV = KHe + KX = KHe + 0,0194KHe => KHe = 5,304 MeV
\( \Rightarrow {v_{He}} = \sqrt {{{2{K_{He}}} \over {{m_{He}}}}} = \sqrt {{{{{2.5,304.1,6.10}^{ - 13}}} \over {{{4,002603.1,66055.10}^{27}}}}} = {16.10^6}m/s\)
Chọn D
Câu hỏi liên quan
-

Ánh sáng trắng là ánh sáng:
-

Một chất điểm dao động điều hòa trên trục Ox với chu kỳ T. Vị trí cân bằng của chất điểm trùng với gốc tọa độ, khoảng thời gian ngắn nhất để nó đi từ vị trí có li độ x = A đến vị trí có li độ x =
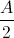 là
là -

Tại sao khi chùm tia sáng mặt trời đi qua một tấm thủy tinh phẳng lại không thấy bị tán sắc thành những màu cơ bản?
-

Dao động của một vật có phương trình: x = acosωt + asinωt. Biên độ dao động của vật là
-

Ánh sáng trắng là :
-

Khi chiếu hai tia sáng đơn sắc song song màu đỏ và màu lục từ không khí vào lăng kính thủy tinh và có tia ló thì:
-

Nguyên nhân sâu xa của hiện tượng tán sắc ánh sáng là sự phụ thuộc của chiết suất môi trường vào:
-

Câu phát biểu nào sau đây về hiện tượng tán sắc là sai ?
-

Chuyển động nào sau đây của chất điểm là một dao động điều hòa?
-

Chọn phát biểu sai?
