Cho lăng trụ tam giác ABC.A’B’C’. Gọi M,N,P lần lượt là trung điểm các cạnh AB; AA’; A’C’. Thiết diện của lăng trụ khi cắt bởi (MNP) là hình gì?
DANH SÁCH CÂU HỎI
-
[Cho lăng trụ tam giác ABC.A’B’C’. Gọi M,N,P lần lượt là trung điểm các cạnh AB; AA’; A’C’. - Luyện Tập 365]
-
[Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC. Khi đó: - Luyện Tập 365]
-
[Trong các mệnh đề sau đây mệnh đề nào đúng? - Luyện Tập 365]
-
[Cho mặt phẳng (P) và hai đường thẳng song song a và b. a.Nếu (P) song song với a thì (P) - Luyện Tập 365]
-
[Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC. Khi đó giao tuyến - Luyện Tập 365]
-
[Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. Trên đoạn BC lấy điểm M sao cho MB=2MC. - Luyện Tập 365]
-
[Cho hình lập phương ABCD.A’B’C’D’. Khi đó AC song song với mặt phẳng nào: - Luyện Tập 365]
-
[Cho hình lập phương ABCD.A’B’C’D’, I và J là tâm của hai hình vuông ABCD và ABB’A’. Khi - Luyện Tập 365]
-
[Cho hình chóp SABCD có đáy là hình thang ABCD, đáy lớn là AD; AD=2BC. Gọi O là giao điểm - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. - Luyện Tập 365]
-
[Cho tứ diện SABC . Trên các cạnh SA và BC lấy 2 điểm M , N sao cho \({{SM} \over {SA}} = - Luyện Tập 365]
-
[CHo tứ diện ABCD với 3 điểm M ,N ,P lần lượt là trung điểm của 3 cạnh BC , BD , AB . Gọi - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình thang , AD // BC , Gọi M là trung điểm của cạnh - Luyện Tập 365]
-
[Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm cạnh SA và O là - Luyện Tập 365]
-
[Cho tứ diện ABCD . Gọi G là trọng tâm của tam giác ACD. Gọi M là điểm trên BC sao cho . - Luyện Tập 365]
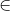AB ). Chứng minh MP // SB 
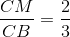. Chứng minh MG // (ABD)