DANH SÁCH CÂU HỎI
-
[Tính diện tích hình thoi BDCH theo R trong trường hợp ∆ABC đều. - Luyện Tập 365]
-
[Cho tam giác MNP cân tại M, đường cao MH ( H ∈ NP). Từ H kẻ HE ⊥ MN ( E ∈ MN). - Luyện Tập 365]
-
[Biết MN = 25cm, HN = 15cm. Tính MH, ME. - Luyện Tập 365]
-
[Đường thẳng đi qua E và song song với NP cắt cạnh MP tại F. Tứ giác NPFE là hình gì? V - Luyện Tập 365]
-
[Cho tam giác ABC (AB < AC) nội tiếp đường tròn tâm O đường kính BC, vẽ AH vuông - Luyện Tập 365]
-
[Chứng minh tứ giác DEHC là tứ giác nội tiếp. - Luyện Tập 365]
-
[Cho tam giác ABC có ba góc ngọn nội tiếp đường tròn O (AB < AC). Hai tiếp tuyến - Luyện Tập 365]
-
[Cho tam giác ABC có ba góc nhọn và H là trực tâm. Vẽ hình bình hành BHCD. Đường thẳ - Luyện Tập 365]
-
[Chứng minh A, B, C, D , E cùng thuộc một đường tròn. - Luyện Tập 365]

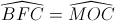
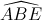 =
=