Trong hình vẽ, ABCD là hình vuông, các đường tròn (A; AB) và (D; DA) cắt nhau tại điểm E (nằm trong hình vuông). Biết cạnh hình vuông bằng 5 cm, tính diện tích các phần được tạo thành.
DANH SÁCH CÂU HỎI
-
[Trong hình vẽ, ABCD là hình vuông, các đường tròn (A; AB) và (D; DA) cắt nhau tại điểm E - Luyện Tập 365]
-
[Cho một tứ giác ABCD và I là giao điểm của các đường chéo. Chứng minh rằng nếu bán kính - Luyện Tập 365]
-
[Từ điểm A ngoài đường tròn (O) kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp - Luyện Tập 365]
-
[Cho tam giác ABC vuông ở A. Nửa đường tròn đường kính AB cắt BC tại D. Trên cung AD lấy - Luyện Tập 365]
-
[Cho tam giác ABC vuông ở A. Nửa đường tròn đường kính AB cắt BC tại D. Trên cung AD lấy - Luyện Tập 365]
-
[Cho tam giác ABC vuông ở A. Nửa đường tròn đường kính AB cắt BC tại D. Trên cung AD lấy - Luyện Tập 365]
-
[Chứng minh CDEF là một tứ giác nội tiếp. - Luyện Tập 365]
-
[Kéo dài DE cắt AC ở K. Tia phân giác của góc CKD cắt EF và CD tại M và N. Tia phân giác - Luyện Tập 365]
-
[Gọi R, R1, R2 theo thứ tự là bán kính đường tròn ngoại tiếp các tam giác ABC, ADB, ADC. - Luyện Tập 365]
-
[Cạnh bên của một tam giác cân bằng 8,0cm, góc ở đáy bằng 30° . Tính độ dài đường kính và - Luyện Tập 365]
-
[Cho tam giác ABC nội tiếp một đường tròn (O). Biết ; AB = a. Tính bán kính đường - Luyện Tập 365]
-
[Hai đường tròn (O; 3,0cm) và (O'; 9,0 cm) tiếp xúc ngoài với nhau. Tính diện tích hình giới - Luyện Tập 365]
-
[Cho tam giác ABC nội tiếp một đường tròn (O) và một điểm M nằm trên (O). Gọi H, I, K theo - Luyện Tập 365]
-
[Cho tam giác ABC cân (AB = AC) ngoại tiếp một đường tròn (O). Gọi các tiếp điểm của (O) - Luyện Tập 365]
-
[Cho tam giác ABC cân (AB = AC) ngoại tiếp một đường tròn (O). Gọi các tiếp điểm của (O) - Luyện Tập 365]
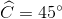; AB = a. Tính bán kính đường tròn (O); độ dài cung nhỏ AB.