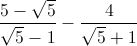Cho a=\frac{1-\sqrt{2}}{2} .Tính giá trị của biểu thức: \sqrt{16a^{8}-51a}
DANH SÁCH CÂU HỎI
-
[Cho a=\frac{1-\sqrt{2}}{2} .Tính giá trị của biểu thức: \sqrt{16a^{8}-51a} - Luyện Tập 365]
-
[Cho a và b là các số thực dương. Chứng minh rằng: (a+b)^{2}+\frac{a+b}{2}\ge - Luyện Tập 365]
-
[Cho n là số nguyên dương và m là ước nguyên dương của - Luyện Tập 365]
-
[Rút gọn biểu thức: A = (√20 - √45 + 3√5).√5 - Luyện Tập 365]
-
[Cho x, y, z là các số thực thỏa mãn điều kiện |x| ≤ 1, |y| ≤ 1, |z| ≤ 1. Chứ - Luyện Tập 365]
-
[Cho a, b, c là các số thực dương. Chứng minh rằng nếu - Luyện Tập 365]
-
[Rút gọn biểu thức sau: N = (12√2 - 3√18 + 2√8) : √2 - Luyện Tập 365]
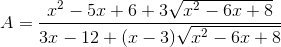
√32 - 2√50 + 
(x ≥ 1)
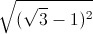- √3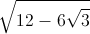
+ 
.
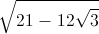
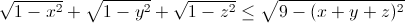
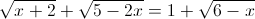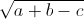= √a + √b - √c thì (a + b – c)2 = a2 + b2 – c2. Điều ngược lại có đúng không? Tại sao?
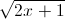có nghĩa với giá trị của x là