Một đồng hồ quả lắc chạy đúng giờ dưới một hầm mỏ có độ sâu h’. Đưa đồng hồ lên mặt đất. Coi nhiệt độ hai nơi này là như nhau. Khi đó đồng hồ sẽ:

Câu hỏi
Nhận biếtMột đồng hồ quả lắc chạy đúng giờ dưới một hầm mỏ có độ sâu h’. Đưa đồng hồ lên mặt đất. Coi nhiệt độ hai nơi này là như nhau. Khi đó đồng hồ sẽ:
Đáp án đúng: A
Lời giải của Luyện Tập 365
Ta có:
\(\eqalign{
& \left\{ \matrix{
g = {{GM} \over {{R^2}}} = {G \over {{R^2}}}.\left( {D.{4 \over 3}\pi {R^3}} \right) = {4 \over 3}\pi .G.D.R \hfill \cr
{g_h} = {{GM'} \over {{{\left( {R - h} \right)}^2}}} = {G \over {{{\left( {R - h} \right)}^2}}}.\left[ {D.{4 \over 3}\pi {{\left( {R - h} \right)}^3}} \right] = {4 \over 3}\pi .G.D.\left( {R - h} \right) \hfill \cr} \right. \cr
& \Rightarrow {g \over {{g_h}}} = {R \over {R - h}} \cr} \)
\(T = 2\pi \sqrt {{l \over g}} \Rightarrow {T \over {{T_h}}} = \sqrt {{{{g_h}} \over g}} = \sqrt {{{R - h} \over R}} = \sqrt {1 - {h \over R}} < 1 \Rightarrow T < {T_h}\)
→ Đồng hồ chạy nhanh
Ta có:
\(\eqalign{
& \left\{ \matrix{
g = {{GM} \over {{R^2}}} = {G \over {{R^2}}}.\left( {D.{4 \over 3}\pi {R^3}} \right) = {4 \over 3}\pi .G.D.R \hfill \cr
{g_h} = {{GM'} \over {{{\left( {R - h} \right)}^2}}} = {G \over {{{\left( {R - h} \right)}^2}}}.\left[ {D.{4 \over 3}\pi {{\left( {R - h} \right)}^3}} \right] = {4 \over 3}\pi .G.D.\left( {R - h} \right) \hfill \cr} \right. \cr
& \Rightarrow {g \over {{g_h}}} = {R \over {R - h}} \cr} \)
\(T = 2\pi \sqrt {{l \over g}} \Rightarrow {T \over {{T_h}}} = \sqrt {{{{g_h}} \over g}} = \sqrt {{{R - h} \over R}} = \sqrt {1 - {h \over R}} < 1 \Rightarrow T < {T_h}\)
→ Đồng hồ chạy nhanh
Câu hỏi liên quan
-

Nguyên nhân sâu xa của hiện tượng tán sắc ánh sáng là sự phụ thuộc của chiết suất môi trường vào:
-

Khi chiếu hai tia sáng đơn sắc song song màu đỏ và màu lục từ không khí vào lăng kính thủy tinh và có tia ló thì:
-

Phát biểu nào sau đây là đúng khi nói về vật dao động điều hòa?
-

Khi chiếu ánh sáng trắng vào một lăng kính thì tia sáng nào bị lệch về phía đáy nhiều nhất ?
-

Một chất điểm dao động điều hòa trên trục Ox với chu kỳ T. Vị trí cân bằng của chất điểm trùng với gốc tọa độ, khoảng thời gian ngắn nhất để nó đi từ vị trí có li độ x = A đến vị trí có li độ x =
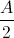 là
là -

Chiếu chùm tia sáng trắng hẹp song song từ không khí tới mặt bên AB của một lăng kính thủy tinh, chùm tia khúc xạ vào trong lăng kính (thuộc một tiết diện thẳng qua lăng kính) truyền tới mặt bên AC, nó khúc xạ tại mặt AC rồi ló ra ngoài không khí. Chùm tia ló bị lệch về phía đáy của lăng kính so với chùm tia tới và tách ra thành một dải nhiều màu khác nhau( như màu cầu vồng), tia tím bị lệch nhiều nhất, tia đỏ bị lệch ít nhất. Hiện tượng đó là :
-

Ánh sáng có tần số lớn nhất trong số các ánh sáng đơn sắc: đỏ, lam, chàm, tím là ánh sáng:
-

Chuyển động nào sau đây của chất điểm là một dao động điều hòa?
-

Dao động của một vật có phương trình: x = acosωt + asinωt. Biên độ dao động của vật là
-

Câu phát biểu nào sau đây về hiện tượng tán sắc là sai ?
