Hai chất điểm M1 và M2 cùng bắt đầu chuyển động từ điểm A dọc theo vòng tròn có bán kính R lần lượt có vận tốc góc ({omega _1} = frac{pi }{3},,rad/s) và ({omega _2} = frac{pi }{6},,rad/s). Gọi P1 và P2 là hai hình chiếu của điểm M1 và M2 trên trục Ox nằm ngang đi qua tâm vòng tròn. Khoảng thời gian ngắn nhất mà hai chất điểm P1 và P2 gặp nhau lại sau đó là

Câu hỏi
Nhận biếtHai chất điểm M1 và M2 cùng bắt đầu chuyển động từ điểm A dọc theo vòng tròn có bán kính R lần lượt có vận tốc góc ({omega _1} = frac{pi }{3},,rad/s) và ({omega _2} = frac{pi }{6},,rad/s). Gọi P1 và P2 là hai hình chiếu của điểm M1 và M2 trên trục Ox nằm ngang đi qua tâm vòng tròn. Khoảng thời gian ngắn nhất mà hai chất điểm P1 và P2 gặp nhau lại sau đó là
Đáp án đúng: C
Lời giải của Luyện Tập 365
Khi M1 và M2 chuyển động dọc theo vòng tròn thì P1 và P2 thực hiện dao động điều hòa trên đường kính vòng tròn dọc theo trục Ox. Chọn điểm A là điểm cắt nhau của vòng tròn với bán trục dương Ox. Khi đó các phương trình dao động của P1 và P2 có dạng : x1 = Rsinω1t và x2 = Rsinω2t. Khi chúng gặp nhau , thì x1 = x2. Vậy để sau khoảng thời gian ngắn nhất P1 và P2 gặp nhau lại , thì giữa ω1 và ω2 phải thỏa mãn điều kiện:
(begin{array}{l}
{omega _1}t = 2pi - {omega _2}t\
Rightarrow left( {{omega _1} + {omega _2}} right)t = 2pi \
Rightarrow left( {frac{pi }{3} + frac{pi }{6}} right).t = 2pi \
Rightarrow t = 4,,left( s right)
end{array})
Khi M1 và M2 chuyển động dọc theo vòng tròn thì P1 và P2 thực hiện dao động điều hòa trên đường kính vòng tròn dọc theo trục Ox. Chọn điểm A là điểm cắt nhau của vòng tròn với bán trục dương Ox. Khi đó các phương trình dao động của P1 và P2 có dạng : x1 = Rsinω1t và x2 = Rsinω2t. Khi chúng gặp nhau , thì x1 = x2. Vậy để sau khoảng thời gian ngắn nhất P1 và P2 gặp nhau lại , thì giữa ω1 và ω2 phải thỏa mãn điều kiện:
(begin{array}{l}
{omega _1}t = 2pi - {omega _2}t\
Rightarrow left( {{omega _1} + {omega _2}} right)t = 2pi \
Rightarrow left( {frac{pi }{3} + frac{pi }{6}} right).t = 2pi \
Rightarrow t = 4,,left( s right)
end{array})
Câu hỏi liên quan
-

Nguyên nhân sâu xa của hiện tượng tán sắc ánh sáng là sự phụ thuộc của chiết suất môi trường vào:
-

Câu nào dưới đây không đúng với vật dao động điều hòa có phương trình x = Acos(
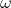 t +
t + 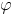 )
) -

Khi chiếu hai tia sáng đơn sắc song song màu đỏ và màu lục từ không khí vào lăng kính thủy tinh và có tia ló thì:
-

Một chất điểm dao động điều hòa trên trục Ox với chu kỳ T. Vị trí cân bằng của chất điểm trùng với gốc tọa độ, khoảng thời gian ngắn nhất để nó đi từ vị trí có li độ x = A đến vị trí có li độ x =
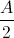 là
là -

Chọn phát biểu sai?
-

Ánh sáng mặt trời là ánh sáng tổng hợp từ bao nhiêu ánh sáng đơn sắc khác nhau ?
-

Một chất điểm dao động điều hòa trên trục Ox. Điểm M nằm trên trục Ox và trong quá trình dao động chất điểm không đi qua M. Tại thời điểm t1 chất điểm ở xa M nhất; tại thời điểm t2 chất điểm ở gần M nhất thì:
-

Dao động của một vật có phương trình: x = acosωt + asinωt. Biên độ dao động của vật là
-

Ánh sáng đơn sắc là ánh sáng:
-

Chọn câu đúng
