Với giá trị nào của m thì hệ có nghiệm duy nhất, hệ vô nghiệm

Câu hỏi
Nhận biếtVới giá trị nào của m thì hệ có nghiệm duy nhất, hệ vô nghiệm
Đáp án đúng: A
Lời giải của Luyện Tập 365
Muốn phương trình đã cho có nghiệm duy nhất thì 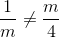
<=> m2 ≠ 4
<=> m ≠ ± 2
Muốn phương trình đã cho có nghiệm thì 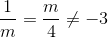 . suy ra m = ± 2 thì hệ vô nghiệm
. suy ra m = ± 2 thì hệ vô nghiệm
Muốn phương trình đã cho có nghiệm duy nhất thì 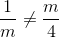
<=> m2 ≠ 4
<=> m ≠ ± 2
Muốn phương trình đã cho có nghiệm thì 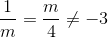 . suy ra m = ± 2 thì hệ vô nghiệm
. suy ra m = ± 2 thì hệ vô nghiệm
Câu hỏi liên quan
-

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Tìm m để phương trình (1) có nghiệm .
-

Giải hệ phương trình với a = 2
-

Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-

Giải phương trình (1) khi m = -5
-

Giải hệ phương trình

-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-

Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
