Vật dao động điều hòa với phương trình x = Acos(8 πt + π/4) tính quãng đường vật đi được sau khoảng thời gian T/4 kể từ thời điểm ban đầu?

Câu hỏi
Nhận biếtVật dao động điều hòa với phương trình x = Acos(8 πt + π/4) tính quãng đường vật đi được sau khoảng thời gian T/4 kể từ thời điểm ban đầu?
Đáp án đúng: D
Phương pháp giải
Ứng dụng đường tròn lượng giác và công thức \(\Delta t = {\alpha \over \omega } = {{\alpha T} \over {2\pi }}\)
Ứng dụng đường tròn lượng giác và công thức \(\Delta t = {\alpha \over \omega } = {{\alpha T} \over {2\pi }}\)
Lời giải của Luyện Tập 365
Phương trình dao động: x = Acos(8πt + π/4)
Góc quét được sau thời gian ∆t = T/4 là \(\alpha = \omega .\Delta t = {{2\pi } \over T}.{T \over 4} = {\pi \over 2}(rad)\)
Thời điểm t = 0 và t = T/4 được biểu diễn trên đường tròn lượng giác:
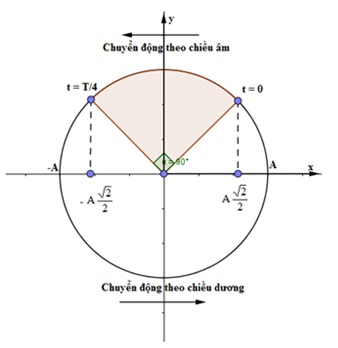
=> Quãng đường vật đi được là: \(S = {A \over {\sqrt 2 }} + {A \over {\sqrt 2 }} = A\sqrt 2 \)
Phương trình dao động: x = Acos(8πt + π/4)
Góc quét được sau thời gian ∆t = T/4 là \(\alpha = \omega .\Delta t = {{2\pi } \over T}.{T \over 4} = {\pi \over 2}(rad)\)
Thời điểm t = 0 và t = T/4 được biểu diễn trên đường tròn lượng giác:

=> Quãng đường vật đi được là: \(S = {A \over {\sqrt 2 }} + {A \over {\sqrt 2 }} = A\sqrt 2 \)
Câu hỏi liên quan
-

Chọn phát biểu sai?
-

Ánh sáng đơn sắc là ánh sáng:
-

Chuyển động nào sau đây của chất điểm là một dao động điều hòa?
-

Dao động điều hòa là
-

Phát biểu nào sau đây sai?
-

Một chùm sáng trắng song song đi từ không khí vào thủy tinh, với góc tới lớn hơn không, sẽ
-

Tại sao khi chùm tia sáng mặt trời đi qua một tấm thủy tinh phẳng lại không thấy bị tán sắc thành những màu cơ bản?
-

Phát biểu nào sau đây là đúng khi nói về vật dao động điều hòa?
-

Câu phát biểu nào sau đây về hiện tượng tán sắc là sai ?
-

Trong chương trình của vật dao động điều hòa x = Acos(ωt + φ), radian trên giây (rad/s) là đơn vị của đại lượng nào sau đây:
