Từ một điểm S nằm ngoài một đường tròn (O), người ta kẻ tới (O) một tiếp tuyến SA và một cát tuyến SBC sao cho 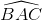 < 90°. Tia phân giác của góc BAC cắt dây BC tại điểm D và cắt đường tròn (O) tại điểm thứ hai E. Các tiếp tuyến của (O) tại C, E cắt nhau tại điểm N. Gọi Q, P theo thứ tự là giao điểm của các cặp đường thẳng AB và CE; AE và CN. Trả lời câu hỏi dưới đây:Chứng minh hệ thức :
< 90°. Tia phân giác của góc BAC cắt dây BC tại điểm D và cắt đường tròn (O) tại điểm thứ hai E. Các tiếp tuyến của (O) tại C, E cắt nhau tại điểm N. Gọi Q, P theo thứ tự là giao điểm của các cặp đường thẳng AB và CE; AE và CN. Trả lời câu hỏi dưới đây:Chứng minh hệ thức : 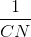 =
= 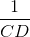 +
+ 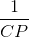

Câu hỏi
Nhận biếtTừ một điểm S nằm ngoài một đường tròn (O), người ta kẻ tới (O) một tiếp tuyến SA và một cát tuyến SBC sao cho ![]() < 90°. Tia phân giác của góc BAC cắt dây BC tại điểm D và cắt đường tròn (O) tại điểm thứ hai E. Các tiếp tuyến của (O) tại C, E cắt nhau tại điểm N. Gọi Q, P theo thứ tự là giao điểm của các cặp đường thẳng AB và CE; AE và CN.
< 90°. Tia phân giác của góc BAC cắt dây BC tại điểm D và cắt đường tròn (O) tại điểm thứ hai E. Các tiếp tuyến của (O) tại C, E cắt nhau tại điểm N. Gọi Q, P theo thứ tự là giao điểm của các cặp đường thẳng AB và CE; AE và CN.
Trả lời câu hỏi dưới đây:
Chứng minh hệ thức : 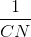 =
= 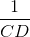 +
+ 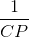
Đáp án đúng: A
Lời giải của Luyện Tập 365
Vì NE, NC đều tiếp xúc (O) nên bằng nhau.
Theo bài 2: EN // CD .
Áp dụng định lí Ta -let, ta có:
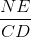 =
= 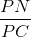 =
= 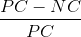 = 1 -
= 1 - 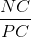
Thay NE bằng NC ta có 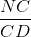 = 1 -
= 1 - 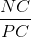
Chia hai vế cho NC rồi chuyển vế sẽ được điều cần chứng minh.
Vì NE, NC đều tiếp xúc (O) nên bằng nhau.
Theo bài 2: EN // CD .
Áp dụng định lí Ta -let, ta có:
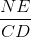 =
= 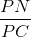 =
= 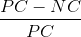 = 1 -
= 1 - 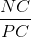
Thay NE bằng NC ta có 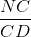 = 1 -
= 1 - 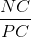
Chia hai vế cho NC rồi chuyển vế sẽ được điều cần chứng minh.
Câu hỏi liên quan
-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Chứng minh rằng: AM2 = AN.AB
-

Tính giá trị biểu thức của A với x =

-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-

Rút gọn A
-

Rút gọn biểu thức A
