Từ điểm B bất kì trên đường tròn tâm O kẻ đường thẳng vuông góc BH với tiếp tuyến của đường tròn tại điểm A cho trước. Gọi I là giao điểm thứ hai của BH với đường tròn (O), gọi B' là điểm đối xứng của điểm B qua tâm O. Trả lời câu hỏi dưới đây:Khi B di động trên đường tròn, chứng minh rằng đường phân giác ngoài của góc OBH đi qua một điểm cố định.
Câu hỏi
Nhận biếtTừ điểm B bất kì trên đường tròn tâm O kẻ đường thẳng vuông góc BH với tiếp tuyến của đường tròn tại điểm A cho trước. Gọi I là giao điểm thứ hai của BH với đường tròn (O), gọi B' là điểm đối xứng của điểm B qua tâm O.
Trả lời câu hỏi dưới đây:
Khi B di động trên đường tròn, chứng minh rằng đường phân giác ngoài của góc OBH đi qua một điểm cố định.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Gọi BA' là đường phân giác của góc ngoài (A' ϵ (O)) của góc OBH
=> Góc A'BA vuông => AA' là đường kính (vì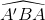 
là góc nội tiếp chắn nửa đường tròn) => điều phải chứng minh.
Gọi BA' là đường phân giác của góc ngoài (A' ϵ (O)) của góc OBH
=> Góc A'BA vuông => AA' là đường kính (vì là góc nội tiếp chắn nửa đường tròn) => điều phải chứng minh.
Câu hỏi liên quan
-
Cho biểu thức A = (
- 
+ 
) : ( x - 2 + 
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-
Chứng minh rằng: AM2 = AN.AB
-
Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-
Tìm m để phương trình (1) có nghiệm .
-
Cho biểu thức:
A =
Trả lời câu hỏi dưới đây:
Rút gọn A
-
Rút gọn A
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Tìm a để phương trình có 2 nghiệm nguyên
-
Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông