Trong trường hợp tứ giác BICD và tứ giác AMPQ đều nội tiếp được thì tam giác ABC là tam giác gì?

Câu hỏi
Nhận biếtTrong trường hợp tứ giác BICD và tứ giác AMPQ đều nội tiếp được thì tam giác ABC là tam giác gì?
Đáp án đúng: D
Lời giải của Luyện Tập 365
Kết hợp các điều kiện trong bài 2 và bài 3 ta có AM // = BC hay BMAC là hình bình hành nội tiếp được nên là hình chữ nhật và 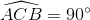
Vậy ∆ ABC vuông ở C.
Kết hợp các điều kiện trong bài 2 và bài 3 ta có AM // = BC hay BMAC là hình bình hành nội tiếp được nên là hình chữ nhật và 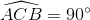
Vậy ∆ ABC vuông ở C.
Câu hỏi liên quan
-

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Giải hệ phương trình với a = 2
-

Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-

Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-

Tìm m để phương trình (1) có nghiệm .
-

Tìm b để A =

-

Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-

Rút gọn A
-

Chứng minh rằng: AM2 = AN.AB
