Trong thí nghiệm Y-âng về giao thoa ánh sáng, khe hẹp S phát ra đồng thời hai bức xạ đơn sắc có bước sóng là λ1 = 4410,0Å và λ2. Trên màn, trong khoảng giữa hai vân sáng liên tiếp có màu giống màu của vân trung tâm còn có chín vân sáng khác. Giá trị của λ2 bằng

Câu hỏi
Nhận biếtTrong thí nghiệm Y-âng về giao thoa ánh sáng, khe hẹp S phát ra đồng thời hai bức xạ đơn sắc có bước sóng là λ1 = 4410,0Å và λ2. Trên màn, trong khoảng giữa hai vân sáng liên tiếp có màu giống màu của vân trung tâm còn có chín vân sáng khác. Giá trị của λ2 bằng
Đáp án đúng: D
Phương pháp giải
Sử dụng lí thuyết về giao thoa đồng thời hai bức xạ đơn sắc
Hai bức xạ trùng nhau: x1 = x2 <=> k1λ1 = k2λ2
Sử dụng lí thuyết về giao thoa đồng thời hai bức xạ đơn sắc
Hai bức xạ trùng nhau: x1 = x2 <=> k1λ1 = k2λ2
Lời giải của Luyện Tập 365
Vị trí vân sáng của hai bức xạ trùng nhau:
\({x_1} = {x_2} \Leftrightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2} \Rightarrow {\lambda _2} = {{{k_1}{\lambda _1}} \over {{k_2}}} = {{{k_1}} \over {{k_2}}}.0,441\left( {\mu m} \right)\)
Trong khoảng giữa hai vân sáng liên tiếp có màu giống màu của vân trung tâm còn có chín vân sáng khác nên ta có:
\({k_1} - 1 + {k_2} - 1 = 9 \Rightarrow {k_1} + {k_2} = 11 \Rightarrow {k_2} = 11 - {k_1} \Rightarrow {\lambda _2} = {{{k_1}.0,441} \over {11 - {k_1}}}\,\,\left( {\mu m} \right)\)
Với:
\(\begin{gathered}
0,38 \leqslant {\lambda _2} \leqslant 0,76 \hfill \\
\Leftrightarrow 0,38 \leqslant \frac{{{k_1}.0,441}}{{11 - {k_1}}} \leqslant 0,76 \hfill \\
\Leftrightarrow 5,09 \leqslant {k_1} \leqslant 6,9 \Rightarrow {k_1} = 6 \Rightarrow {k_2} = 5 \hfill \\
\Rightarrow {\lambda _2} = 5292{A^0} \hfill \\
\end{gathered} \)
Chọn D.
Vị trí vân sáng của hai bức xạ trùng nhau:
\({x_1} = {x_2} \Leftrightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2} \Rightarrow {\lambda _2} = {{{k_1}{\lambda _1}} \over {{k_2}}} = {{{k_1}} \over {{k_2}}}.0,441\left( {\mu m} \right)\)
Trong khoảng giữa hai vân sáng liên tiếp có màu giống màu của vân trung tâm còn có chín vân sáng khác nên ta có:
\({k_1} - 1 + {k_2} - 1 = 9 \Rightarrow {k_1} + {k_2} = 11 \Rightarrow {k_2} = 11 - {k_1} \Rightarrow {\lambda _2} = {{{k_1}.0,441} \over {11 - {k_1}}}\,\,\left( {\mu m} \right)\)
Với:
\(\begin{gathered}
0,38 \leqslant {\lambda _2} \leqslant 0,76 \hfill \\
\Leftrightarrow 0,38 \leqslant \frac{{{k_1}.0,441}}{{11 - {k_1}}} \leqslant 0,76 \hfill \\
\Leftrightarrow 5,09 \leqslant {k_1} \leqslant 6,9 \Rightarrow {k_1} = 6 \Rightarrow {k_2} = 5 \hfill \\
\Rightarrow {\lambda _2} = 5292{A^0} \hfill \\
\end{gathered} \)
Chọn D.
Câu hỏi liên quan
-

Ánh sáng mặt trời là ánh sáng tổng hợp từ bao nhiêu ánh sáng đơn sắc khác nhau ?
-

Phát biểu nào sau đây là đúng khi nói về vật dao động điều hòa?
-

Ánh sáng trắng là ánh sáng:
-

Khi chiếu ánh sáng trắng vào một lăng kính thì tia sáng nào bị lệch về phía đáy nhiều nhất ?
-

Câu phát biểu nào sau đây về hiện tượng tán sắc là sai ?
-

Phát biểu nào dưới đây là sai khi nói về ánh sáng trắng và ánh sáng đơn sắc:
-

Một vật nhỏ dao động điều hòa theo một trục cố định. Phát biểu nào sau đây đúng?
-

Câu nào dưới đây không đúng với vật dao động điều hòa có phương trình x = Acos(
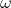 t +
t + 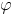 )
) -

Dao động điều hòa là
-

Phát biểu nào sau đây là không đúng? Gia tốc của một vật dao động điều hòa
