Trong tháng giêng hai tổ sản xuất được 720 chi tiết máy, tháng hai tổ một vượt 12%, tổ 2 vượt 15% nên sản xuất được 819 chi tiết máy. Tính xem tháng giêng mỗi tổ sản xuất được bao nhiêu chi tiết máy?

Câu hỏi
Nhận biếtTrong tháng giêng hai tổ sản xuất được 720 chi tiết máy, tháng hai tổ một vượt 12%, tổ 2 vượt 15% nên sản xuất được 819 chi tiết máy. Tính xem tháng giêng mỗi tổ sản xuất được bao nhiêu chi tiết máy?
Đáp án đúng: D
Lời giải của Luyện Tập 365
Gọi x là số chi tiết máy tổ một sản xuất trong tháng giêng, gọi y là số chi tiết máy tổ hai sản xuất được trong tháng giêng; x, y nguyên dương, x < 720, y < 720.
Vậy có hệ phương trình: 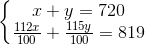
Giải hệ phương trình này ta tìm được nghiệm của hệ là: x = 300 và y = 420
Kết luận: x = 300 và y = 420 thỏa mãn điều kiện bài toán nên trong tháng giêng tổ một sản xuất được 300 chi tiết máy, tổ hai sản xuất được 420 chi tiết máy.
Gọi x là số chi tiết máy tổ một sản xuất trong tháng giêng, gọi y là số chi tiết máy tổ hai sản xuất được trong tháng giêng; x, y nguyên dương, x < 720, y < 720.
Vậy có hệ phương trình: 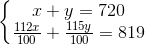
Giải hệ phương trình này ta tìm được nghiệm của hệ là: x = 300 và y = 420
Kết luận: x = 300 và y = 420 thỏa mãn điều kiện bài toán nên trong tháng giêng tổ một sản xuất được 300 chi tiết máy, tổ hai sản xuất được 420 chi tiết máy.
Câu hỏi liên quan
-

Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Tính AC và BD biết
 =
=  . Chứng tỏ tích AC.BD không phụ thuộc vào
. Chứng tỏ tích AC.BD không phụ thuộc vào 
-

Chứng minh rằng: AM2 = AN.AB
-

Tìm b để A =

-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

Giải hệ phương trình

-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
