Trong mặt phẳng tọa độ Oxy cho elip (E): x2 + 9y2 = 0. Tìm tất cả các điểm thuộc (E) sao cho khoảng cách từ mỗi điểm tới 2 tiêu điểm F1 lớn nhất; nhỏ nhất.
Câu hỏi
Nhận biếtTrong mặt phẳng tọa độ Oxy cho elip (E): x2 + 9y2 = 0. Tìm tất cả các điểm thuộc (E) sao cho khoảng cách từ mỗi điểm tới 2 tiêu điểm F1 lớn nhất; nhỏ nhất.
Đáp án đúng: D
Lời giải của Luyện Tập 365
Gọi M0 (x0 ;y0) ∈ (E)=> x02 + 9y02 = 9
Vì x02 ≤ x02 + 9y02 = 9 => - 3 ≤ x0 ≤ 3 (*)
Ta có: a = 3; b = 1; c = 2 √2 nên:
Gọi M0 (x0 ;y0) ∈ (E) => x02 + 9y02 = 9 Vì x02 ≤ x02 + 9y02 = 9 => - 3 ≤ x0 ≤ 3 Ta có: a = 3; b = 1; c = 2 √2 nên: M0 F1 = 3 +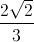 
x0
M0 F1 là hàm số đồng biến với biến số x0
Kết hợp với (*) => 3 - 2√2 ≤ M0 F1 ≤ 3 + 2√2
=> max M0 F1 = 3 + 2√2 khi x0 = 3 => y0 = 0
min M0 F1 = 3 - 2√2 khi x0 = -3 => y0 = 0.
=> M0(3 ; 0) thì M0 F1 đạt giá trị lớn nhất;
M0(-3 ; 0) đạt giá trị nhỏ nhất.
Gọi M0 (x0 ;y0) ∈ (E)=> x02 + 9y02 = 9
Vì x02 ≤ x02 + 9y02 = 9 => - 3 ≤ x0 ≤ 3 (*)
Ta có: a = 3; b = 1; c = 2 √2 nên:
Gọi M0 (x0 ;y0) ∈ (E) => x02 + 9y02 = 9 Vì x02 ≤ x02 + 9y02 = 9 => - 3 ≤ x0 ≤ 3 Ta có: a = 3; b = 1; c = 2 √2 nên: M0 F1 = 3 + 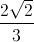x0
M0 F1 là hàm số đồng biến với biến số x0
Kết hợp với (*) => 3 - 2√2 ≤ M0 F1 ≤ 3 + 2√2
=> max M0 F1 = 3 + 2√2 khi x0 = 3 => y0 = 0
min M0 F1 = 3 - 2√2 khi x0 = -3 => y0 = 0.
=> M0(3 ; 0) thì M0 F1 đạt giá trị lớn nhất;
M0(-3 ; 0) đạt giá trị nhỏ nhất.
Câu hỏi liên quan
-
Trong mặt phẳng với hệ trục Oxy, cho hình thoi ABCD biết phương trình của một đường chéo là 3x+y-7=0, điểm B(0;-3), diện tích hình thoi bằng 20. Tìm tọa độ các đỉnh còn lại của hình thoi.
-
Giải phương trình:
-
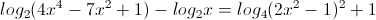
Tìm số phức z thỏa mãn
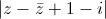= √5 và (2 - z)(i + 
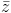) là số ảo. -
Cho các số thực x, y thỏa mãn điều kiện x+y=
+
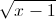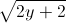Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=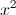
+
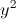+2(x+1)(y+1)+8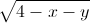
-
Cho các số thực x,y thỏa mãn x
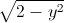+ y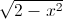
= 2 Tìm giá trị lớn nhất của biểu thức P=
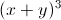-12(x-1).(y-1)+√xy. -
Giải phương trình (1-
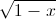).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif)
= x. -
Giải hệ phương trình
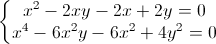(x, y
R) -
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng 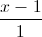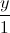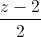d:
=
=
, d':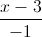
=
=
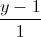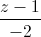và tạo với đường thẳng d một góc 
. -
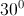Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-
Tìm số phức z thỏa mãn
+
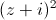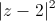=2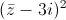
.