Trong mặt phẳng 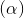 cho góc xOy . Gọi At là nửa đường thẳng nằm ngoài mặt phẳng
cho góc xOy . Gọi At là nửa đường thẳng nằm ngoài mặt phẳng 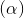 sao cho At song song và cùng chiều với Ox . Xét 3 điểm di động M , E, N lần lượt thuộc Ox , At , Oy sao cho OM = AE = ON
a) Chứng minh (MNE) luôn song song với 1 mặt phẳng cố định
b) Gọi I ; J ; K lần lượt là trung điểm của OA ; ME ; NE . Chứng minh (IJK) //
sao cho At song song và cùng chiều với Ox . Xét 3 điểm di động M , E, N lần lượt thuộc Ox , At , Oy sao cho OM = AE = ON
a) Chứng minh (MNE) luôn song song với 1 mặt phẳng cố định
b) Gọi I ; J ; K lần lượt là trung điểm của OA ; ME ; NE . Chứng minh (IJK) // 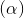

Câu hỏi
Nhận biếtTrong mặt phẳng 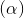 cho góc xOy . Gọi At là nửa đường thẳng nằm ngoài mặt phẳng
cho góc xOy . Gọi At là nửa đường thẳng nằm ngoài mặt phẳng 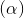 sao cho At song song và cùng chiều với Ox . Xét 3 điểm di động M , E, N lần lượt thuộc Ox , At , Oy sao cho OM = AE = ON
sao cho At song song và cùng chiều với Ox . Xét 3 điểm di động M , E, N lần lượt thuộc Ox , At , Oy sao cho OM = AE = ON
a) Chứng minh (MNE) luôn song song với 1 mặt phẳng cố định
b) Gọi I ; J ; K lần lượt là trung điểm của OA ; ME ; NE . Chứng minh (IJK) // 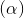
Đáp án đúng:
Lời giải của Luyện Tập 365
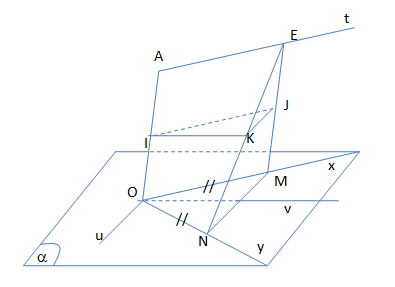
a) Ta có OAEM là hình bình hành => ME // OA
Kẻ tia phân giác ngoài và tia phân giác trong Ou ; Ov của góc xOy.
Vì tam giác OMN cân tại O nên: MN 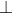 Ov => Mn // Ou
Ov => Mn // Ou
Vậy (MNE) // (Ou ; OA) cố định.
b) Ta có : IJ // OM => IJ // 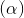
KJ // NM => KJ // 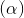 => (IJK) //
=> (IJK) // 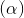

a) Ta có OAEM là hình bình hành => ME // OA
Kẻ tia phân giác ngoài và tia phân giác trong Ou ; Ov của góc xOy.
Vì tam giác OMN cân tại O nên: MN 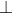 Ov => Mn // Ou
Ov => Mn // Ou
Vậy (MNE) // (Ou ; OA) cố định.
b) Ta có : IJ // OM => IJ // 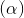
KJ // NM => KJ // 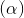 => (IJK) //
=> (IJK) // 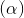
Câu hỏi liên quan
-

-

Tìm số hạng không chứa x trong khai triển của nhị thức
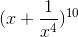
-

-

-

-

Tìm số hạng không chứa x trong khai triển của nhị thức
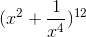
-

Có bao nhiêu cách sắp xếp 5 bạn học sinh A, B, C, D, E ngồi vào một chiếc ghế dài sao cho:
a. Bạn C ngồi chính giữa?
b. Hai bạn A và E ngồi ở hai đầu ghế?
-

-

-

Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?