Trong mặt phẳng cho 2010 điểm phân biệt sao cho không có 3 điểm nào thẳng hàng và không có 4 điểm nào cùng nằm trên một đường tròn. Chứng minh rằng trong 2010 điểm đã cho, có thể dựng được một bộ đường tròn đi qua 3 điểm, chứa 1000 điểm và không chứa 1007 điểm còn lại.
Câu hỏi
Nhận biếtTrong mặt phẳng cho 2010 điểm phân biệt sao cho không có 3 điểm nào thẳng hàng và không có 4 điểm nào cùng nằm trên một đường tròn. Chứng minh rằng trong 2010 điểm đã cho, có thể dựng được một bộ đường tròn đi qua 3 điểm, chứa 1000 điểm và không chứa 1007 điểm còn lại.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Vì các điểm đã cho là hữu hạn nên tồn tại hai điểm A, B sao cho 2008 điểm còn lại nằm về một phía đối với đường thẳng AB.
Do không có 4 điểm nào nằm cùng trên một đường tròn nên ta có thể đặt tên 2008 điểm còn lại là M1, M2, ......, M 2008 sao cho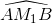 
> 
> .....> 
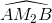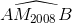
Vẽ đường tròn đi qua A, B, M1001 .
Khi đó các điểm M1, M2, ......, M1000 nằm trong đường tròn này và các điểm còn lại nằm ngoài đường tròn này.
Vì các điểm đã cho là hữu hạn nên tồn tại hai điểm A, B sao cho 2008 điểm còn lại nằm về một phía đối với đường thẳng AB.
Do không có 4 điểm nào nằm cùng trên một đường tròn nên ta có thể đặt tên 2008 điểm còn lại là M1, M2, ......, M 2008 sao cho > > .....>
Vẽ đường tròn đi qua A, B, M1001 .
Khi đó các điểm M1, M2, ......, M1000 nằm trong đường tròn này và các điểm còn lại nằm ngoài đường tròn này.
Câu hỏi liên quan
-
Cho biểu thức:
A =
Trả lời câu hỏi dưới đây:
Rút gọn A
-
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-
Cho biểu thức A = (
- 
+ 
) : ( x - 2 + 
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-
Giải hệ phương trình với a = 2
-
AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-
Cho nửa đường tròn (O), đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E khắc với điểm A. Từ các điểm E, A và B kẻ các tiếp tuyến của nửa đường tròn (O). Tiếp tuyến kẻ từ E lần lượt cắt các tiếp tuyến từ điểm A và B tại C và D.
Trả lời câu hỏi dưới đây:
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-
Chứng minh rằng: AM2 = AN.AB
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.