Trong dãy số gồm 2010 số thực khác 0 được sắp xếp theo thứ tự 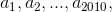 ta đánh dấu tất cả các số dương và tất cả các số mà tổng của nó với một số liên tiếp liền ngay sau nó là một số dương. Ví dụ với dãy số -8, -4, 5, -1, 2, -1, -2, -3, ...., -2005 thì các số được đánh dấu là
ta đánh dấu tất cả các số dương và tất cả các số mà tổng của nó với một số liên tiếp liền ngay sau nó là một số dương. Ví dụ với dãy số -8, -4, 5, -1, 2, -1, -2, -3, ...., -2005 thì các số được đánh dấu là 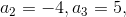
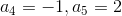 Chứng minh rằng nếu trong dãy đã cho có ít nhất một số dương thì tổng của tất cả các số được đánh dấu là một số dương.
Chứng minh rằng nếu trong dãy đã cho có ít nhất một số dương thì tổng của tất cả các số được đánh dấu là một số dương.

Câu hỏi
Nhận biếtTrong dãy số gồm 2010 số thực khác 0 được sắp xếp theo thứ tự 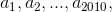 ta đánh dấu tất cả các số dương và tất cả các số mà tổng của nó với một số liên tiếp liền ngay sau nó là một số dương. Ví dụ với dãy số -8, -4, 5, -1, 2, -1, -2, -3, ...., -2005 thì các số được đánh dấu là
ta đánh dấu tất cả các số dương và tất cả các số mà tổng của nó với một số liên tiếp liền ngay sau nó là một số dương. Ví dụ với dãy số -8, -4, 5, -1, 2, -1, -2, -3, ...., -2005 thì các số được đánh dấu là 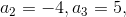
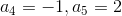
Chứng minh rằng nếu trong dãy đã cho có ít nhất một số dương thì tổng của tất cả các số được đánh dấu là một số dương.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Nếu tất cả các số là số dương thì suy ra đpcm.
Xét trường hợp tồn tại i để 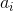 được đánh dấu và
được đánh dấu và 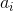 < 0, chọn i là chỉ số nhỏ nhất như vậy.
< 0, chọn i là chỉ số nhỏ nhất như vậy.
Khi đó theo giả thiết tồn tại k để 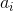 > 0
> 0
Giả sử k là số nhỏ nhất để 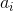 > 0 (1)
> 0 (1)
(hiển nhiên k ≥ 1).
Như vậy:
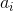 < 0
< 0
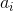 ≤ 0
≤ 0
...........
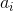 ≤ 0
≤ 0
Ta có 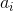 > 0 =>
> 0 => 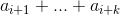 > 0
> 0
=> 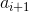 được đánh dấu.
được đánh dấu.
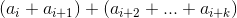 > 0 =>
> 0 => 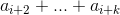 > 0
> 0
=> 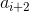 được đánh dấu.
được đánh dấu.
..............
Cuối cùng 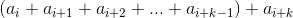 > 0 =>
> 0 => 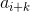 > 0
> 0
=> 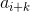 cũng được đánh dấu.
cũng được đánh dấu.
Suy ra tất cả các số 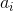 đều được đánh dấu.
đều được đánh dấu.
Như vậy, trong các số 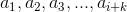 các số được đánh dấu có tổng lớn hơn 0.
các số được đánh dấu có tổng lớn hơn 0.
Tiếp tục quá trình lập luận như trên cho các số còn lại 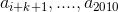 . Sau một số hữu hạn bước ta được đpcm.
. Sau một số hữu hạn bước ta được đpcm.
Nếu tất cả các số là số dương thì suy ra đpcm.
Xét trường hợp tồn tại i để 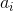 được đánh dấu và
được đánh dấu và 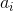 < 0, chọn i là chỉ số nhỏ nhất như vậy.
< 0, chọn i là chỉ số nhỏ nhất như vậy.
Khi đó theo giả thiết tồn tại k để 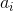 > 0
> 0
Giả sử k là số nhỏ nhất để 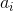 > 0 (1)
> 0 (1)
(hiển nhiên k ≥ 1).
Như vậy:
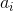 < 0
< 0
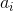 ≤ 0
≤ 0
...........
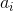 ≤ 0
≤ 0
Ta có 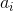 > 0 =>
> 0 => 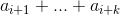 > 0
> 0
=> 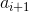 được đánh dấu.
được đánh dấu.
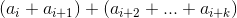 > 0 =>
> 0 => 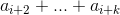 > 0
> 0
=> 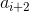 được đánh dấu.
được đánh dấu.
..............
Cuối cùng 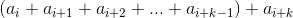 > 0 =>
> 0 => 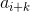 > 0
> 0
=> 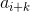 cũng được đánh dấu.
cũng được đánh dấu.
Suy ra tất cả các số 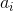 đều được đánh dấu.
đều được đánh dấu.
Như vậy, trong các số 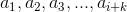 các số được đánh dấu có tổng lớn hơn 0.
các số được đánh dấu có tổng lớn hơn 0.
Tiếp tục quá trình lập luận như trên cho các số còn lại 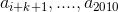 . Sau một số hữu hạn bước ta được đpcm.
. Sau một số hữu hạn bước ta được đpcm.
Câu hỏi liên quan
-

Giải hệ phương trình

-

Chứng minh DM.CE=DE.CM
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-

Tìm b để A =

-

Tính giá trị biểu thức của A với x =

-

Rút gọn A
-

Giải phương trình (1) khi m = -5
-

Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
