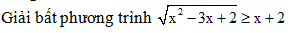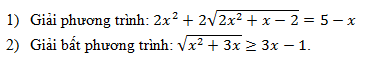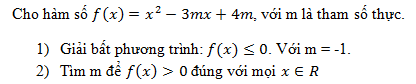Trình bày cách nhẩm nghiệm cho các phương trình sau:
a. 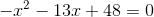 b.
b. 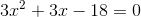 c.
c. 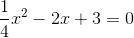

Câu hỏi
Nhận biếtTrình bày cách nhẩm nghiệm cho các phương trình sau:
a. 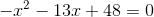
b. 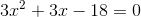
c. 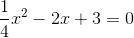
Đáp án đúng:
Lời giải của Luyện Tập 365
a. Viết lại phương trình dưới dạng: 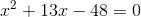
Khi đó:
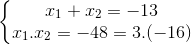
mà 3 + (-16)=-13
Vậy, phương trình có hai nghiệm: 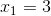 và
và 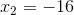
b. Viết lại phương trình dưới dạng: 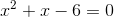
Khi đó:
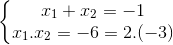
mà 2 + (-3)=-1
Vậy, phương trình có hai nghiệm: 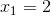 và
và 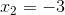
c. Viết lại phương trình dưới dạng: 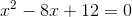
Khi đó:
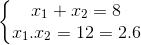
mà 2+6=8.
Vậy, phương trình có hai nghiệm: 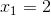 và
và 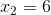
a. Viết lại phương trình dưới dạng: 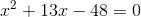
Khi đó:
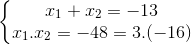
mà 3 + (-16)=-13
Vậy, phương trình có hai nghiệm: 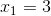 và
và 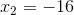
b. Viết lại phương trình dưới dạng: 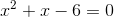
Khi đó:
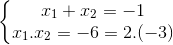
mà 2 + (-3)=-1
Vậy, phương trình có hai nghiệm: 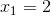 và
và 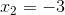
c. Viết lại phương trình dưới dạng: 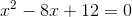
Khi đó:
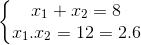
mà 2+6=8.
Vậy, phương trình có hai nghiệm: 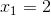 và
và 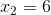
Câu hỏi liên quan
-

Giải và biện luận phương trình sau theo tham số m
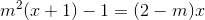
-

Dùng định nghĩa để tìm khoảng tăng giảm của hàm số:
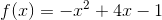
-

Cho góc
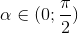 thỏa mãn
thỏa mãn 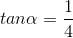 .. Tính các giá trị lượng giác còn lại của
.. Tính các giá trị lượng giác còn lại của 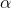
-

-

Xác định hàm số bậc hai
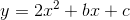 biết rằng đồ thị của nó có hoành độ đỉnh là 2 và đị qua điểm M(1;-2)
biết rằng đồ thị của nó có hoành độ đỉnh là 2 và đị qua điểm M(1;-2) -

BAN NÂNG CAO
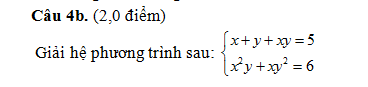
-

Dùng định nghĩa để xác định khoảng tăng giảm của hàm số sau:
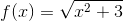
-

-

Tìm tập xác định của hàm số sau;
a)
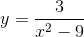
b)
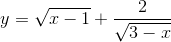
c)
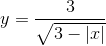
-

Phần nâng cao