Trên nửa mặt phẳng bờ AB chứa điểm M. Hãy dựng một đường tròn có đường kính bằng 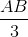 sao cho nó không có điểm chung với đường thẳng HI với mọi vị trí của điểm M trên nửa đường tròn (O).
sao cho nó không có điểm chung với đường thẳng HI với mọi vị trí của điểm M trên nửa đường tròn (O).

Câu hỏi
Nhận biếtTrên nửa mặt phẳng bờ AB chứa điểm M. Hãy dựng một đường tròn có đường kính bằng 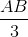 sao cho nó không có điểm chung với đường thẳng HI với mọi vị trí của điểm M trên nửa đường tròn (O).
sao cho nó không có điểm chung với đường thẳng HI với mọi vị trí của điểm M trên nửa đường tròn (O).
Đáp án đúng: A
Lời giải của Luyện Tập 365
sđ cung HI = 90° => 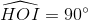 => ∆ OHI là tam giác vuông cân.
=> ∆ OHI là tam giác vuông cân.
Hạ OS ┴ HI tại S => ∆ OSI vuông cân nên OS = SI = 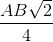
và đường tròn (O; 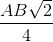 ) luôn luôn tiếp xúc với HI tại S. Dựng OO1 ┴ AB sao cho
) luôn luôn tiếp xúc với HI tại S. Dựng OO1 ┴ AB sao cho 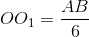 rồi dựng đường tròn (
rồi dựng đường tròn (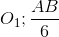 ). Chỉ cần (
). Chỉ cần (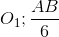 ) nằm trong (O;
) nằm trong (O; 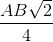 ) là đủ để HI, (
) là đủ để HI, (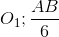 ) không có điểm chung. Quả vậy,
) không có điểm chung. Quả vậy, 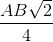

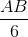 =
= 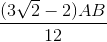 >
> 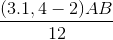 >
> 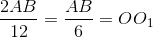 . Và (
. Và (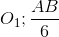 ) chính là một đường tròn cần dựng.
) chính là một đường tròn cần dựng.
sđ cung HI = 90° => 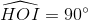 => ∆ OHI là tam giác vuông cân.
=> ∆ OHI là tam giác vuông cân.
Hạ OS ┴ HI tại S => ∆ OSI vuông cân nên OS = SI = 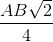
và đường tròn (O; 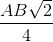 ) luôn luôn tiếp xúc với HI tại S. Dựng OO1 ┴ AB sao cho
) luôn luôn tiếp xúc với HI tại S. Dựng OO1 ┴ AB sao cho 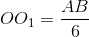 rồi dựng đường tròn (
rồi dựng đường tròn (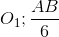 ). Chỉ cần (
). Chỉ cần (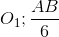 ) nằm trong (O;
) nằm trong (O; 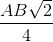 ) là đủ để HI, (
) là đủ để HI, (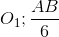 ) không có điểm chung. Quả vậy,
) không có điểm chung. Quả vậy, 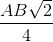

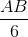 =
= 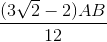 >
> 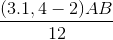 >
> 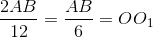 . Và (
. Và (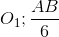 ) chính là một đường tròn cần dựng.
) chính là một đường tròn cần dựng.
Câu hỏi liên quan
-

Chứng minh rằng: AM2 = AN.AB
-

Giải hệ phương trình với a = 2
-

Giải hệ phương trình

-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Chứng minh DM.CE=DE.CM
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-

Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
