Tính khoảng cách từ bảng gỗ đến bức tường lúc bảng chạm bóng lần thứ n. Khi đó bóng đã đi thêm được một quãng đường bao nhiêu kể từ va chạm lần thứ nhất? Chứng minh rằng khi chạm bảng gỗ chạm vào tường (bỏ qua kích thước rất nhỏ của bóng) thì số lần bóng đã đập lên bảng gỗ không phụ thuộc vào các đại lượng v0; v1; l1.(HS tự giải).

Câu hỏi
Nhận biếtTính khoảng cách từ bảng gỗ đến bức tường lúc bảng chạm bóng lần thứ n. Khi đó bóng đã đi thêm được một quãng đường bao nhiêu kể từ va chạm lần thứ nhất?
Chứng minh rằng khi chạm bảng gỗ chạm vào tường (bỏ qua kích thước rất nhỏ của bóng) thì số lần bóng đã đập lên bảng gỗ không phụ thuộc vào các đại lượng v0; v1; l1.(HS tự giải).
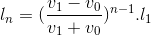
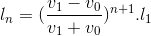
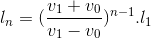
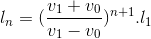
Đáp án đúng: A
Lời giải của Luyện Tập 365
1)
Xét lần va chạm thứ 3.
Gọi l3 là khoảng cách tù bảng đến tường khi xảy ra va chạm lần 3. Tương tụ câu a) với l3 lúc này có vai trò l2 ở câu a; l2 lúc này có vai trò như l1 ở câu a), ta có:
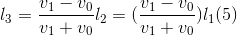
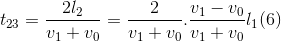
Xét lần va chạm thứ tư:
Tương tự như trên, ta có: 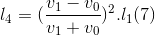
Và 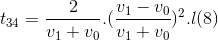
....
Xét lần va chạm thứ n, bóng cách tường một đoạn
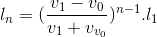 (9). Và
(9). Và 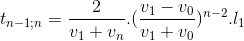 (10)
(10)
Thời gian trôi qua kể từ va chạm lần 1 đến va chạm lần thứ n là
t = t12 + t23 + … + tn – 1; n
![=\frac{2l_{1}}{v_{1}+v_{0}}[(\frac{v_{1}-v_{0}}{v_{1}+v_{0}})^{2}]+(\frac{v_{1}-v_{0}}{v_{1}+v_{0}})^{2}+(\frac{v_{1}-v_{0}}{v_{1}+v_{0}})^{2}+...+(\frac{v_{1}-v_{0}}{v_{1}+v_{0}})^{n-2}]](https://luyentap365.com/wp-content/picture/learning/exam/2014/0228/v23547_633820_7.gif)
Vậy quãng đường bóng đi được từ va chạm lần 1 đến va chạm lần thứ n là:
![S=v_{1}t=\frac{2v_{1}}{v_{1}+v_{0}}[\sum_{k=0}^{n-2}\left ( \frac{v_{1}-v_{0}}{v_{1}+v_{0}} \right )^{k}].l_{1}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0228/v23547_683676_8.gif)
2, Chứng minh
Giả sử bảng va chạm vào tường ở lần thứ k bóng va chạm với bảng mà k là một số hữu hạn thì: 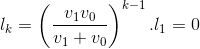
Vì (v1 – v0) > 0 nên l1 = 0 (vô lý).
Vậy sau vô số lần va chạm giữa bóng và bảng gỗ thì bảng mới chạm vào tường, tức là số lần va chạm luôn luôn là rất lớn, không phụ thuộc vào v0, v1, l1.
1)
Xét lần va chạm thứ 3.
Gọi l3 là khoảng cách tù bảng đến tường khi xảy ra va chạm lần 3. Tương tụ câu a) với l3 lúc này có vai trò l2 ở câu a; l2 lúc này có vai trò như l1 ở câu a), ta có:
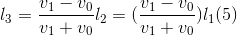
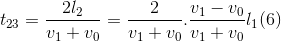
Xét lần va chạm thứ tư:
Tương tự như trên, ta có: 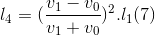
Và 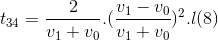
....
Xét lần va chạm thứ n, bóng cách tường một đoạn
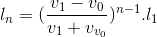 (9). Và
(9). Và 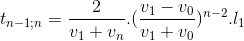 (10)
(10)
Thời gian trôi qua kể từ va chạm lần 1 đến va chạm lần thứ n là
t = t12 + t23 + … + tn – 1; n
![=\frac{2l_{1}}{v_{1}+v_{0}}[(\frac{v_{1}-v_{0}}{v_{1}+v_{0}})^{2}]+(\frac{v_{1}-v_{0}}{v_{1}+v_{0}})^{2}+(\frac{v_{1}-v_{0}}{v_{1}+v_{0}})^{2}+...+(\frac{v_{1}-v_{0}}{v_{1}+v_{0}})^{n-2}]](https://luyentap365.com/wp-content/picture/learning/exam/2014/0228/v23547_633820_7.gif)
Vậy quãng đường bóng đi được từ va chạm lần 1 đến va chạm lần thứ n là:
![S=v_{1}t=\frac{2v_{1}}{v_{1}+v_{0}}[\sum_{k=0}^{n-2}\left ( \frac{v_{1}-v_{0}}{v_{1}+v_{0}} \right )^{k}].l_{1}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0228/v23547_683676_8.gif)
2, Chứng minh
Giả sử bảng va chạm vào tường ở lần thứ k bóng va chạm với bảng mà k là một số hữu hạn thì: 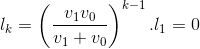
Vì (v1 – v0) > 0 nên l1 = 0 (vô lý).
Vậy sau vô số lần va chạm giữa bóng và bảng gỗ thì bảng mới chạm vào tường, tức là số lần va chạm luôn luôn là rất lớn, không phụ thuộc vào v0, v1, l1.
Câu hỏi liên quan
-

Điều chỉnh con chạy C để đèn sáng bình thường, hỏi con chạy C đã chia biến trở thành hai phần có tỉ lệ như thế nào?
-

Thay ampe kế bằng vôn kế có điện trở vô cùng lớn. Tìm R3 để số chỉ vôn kế là 16V. Nếu di chuyển con chạy để R3 tăng lên thì số chỉ của vôn kế thay đổi như thế nào?
-

Thay ròng rọc cố định R bằng một Pa-lăng gồm một ròng rọc cố định R và một ròng rọc cố định R’, đồng thời di chuyển vị trí đứng của người đó về điểm I sao cho
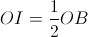 (Hình 2) . Người đó phải tác dụng vào dây một lực F bằng bao nhiêu để tấm ván OB nằm ngang thăng bằng ? Tính lực F’ do ván tác dụng vào điểm tựa O ? (Bỏ qua ma sát ở các ròng rọc và trọng lượng của dây, của ròng rọc)
(Hình 2) . Người đó phải tác dụng vào dây một lực F bằng bao nhiêu để tấm ván OB nằm ngang thăng bằng ? Tính lực F’ do ván tác dụng vào điểm tựa O ? (Bỏ qua ma sát ở các ròng rọc và trọng lượng của dây, của ròng rọc) -

Để cục nước đá chuyển hoàn toàn sang thể hơi ở 1000C thì cần một nhiệt lượng là bao nhiêu kJ? Cho nhiệt dung riêng của nước và nước đá là C1 = 4200J/kg.K; C2 = 1800J/kg.K. Nhiệt nóng chảy của nước đá là λ = 3,4.105 J/kg; nhiệt hóa hơi của nước là L = 2,3.106 j/kg.(Bỏ qua sự mất nhiệt với môi trường ngoài).
-

Sau thấu kính L1 người ta đặt một thấu kính phân kì L2 có tiêu cự f2 = . Thấu kính L2 cách thấu kính L1 một khoảng O1O2 = , trục chính của thấu kính trùng nhau (Hình vẽ 3). Vẽ ảnh của vật AB qua hai thấu kính trên và dùng hình học ( không dùng công thức thấu kính) tìm khoảng cách từ ảnh cuối cùng A2B2 đến thấu kính phân kỳ.
-

Sau khi đổ đầy vào dầu nhánh B, người ta thả nhẹ nhàng một vật hình trụ đặc, đồng chất tiết diện S3 = 60cm3, cao h3 = 10cm, khối lượng riêng D3 = 600kg/m3 vào nhánh A. Hãy tính khối lượng dầu tràn ra ngoài.
-

Điều chỉnh Rx để công suất tiêu thụ trên đèn bằng 9W. Tìm công suất trên R2 theo k.
-

Xác định x theo L, để cho cường độ dòng điện trong mạch chính đạt : a, Cực tiểu. b, Cực đại.
-

Tính khối lượng dầu đã đổ vào nhánh B.
-

Vẽ một tia sáng phát ra từ A sau khi đi qua hai thấu kính thì tia ló có phương đi qua B.
