Tìm giá trị của y thỏa mãn: A√y = 2√y – 3 -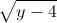 
.
Câu hỏi
Nhận biếtTìm giá trị của y thỏa mãn: A√y = 2√y – 3 - .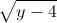
Đáp án đúng: B
Lời giải của Luyện Tập 365
A√y = 2√y – 3 –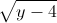
⇔ 
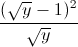√y = 6√y – 3 –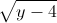
(√y)2 - 2√y + 1 - 2√y + 3 = -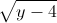
(√y)2 - 4√y + 4 = -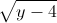
(√y – 2)2 = -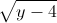
Ta có (√y – 2)2 ≥ 0 với ∀y ∈ TXĐ. Dấu “=” xảy ra khi √y – 2 = 0 ⇔ y = 4
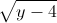- ≤ 0 với ∀y ∈ TXĐ. Dấu “=” xảy ra khi y – 4 = 0 ⇔ y = 4.
Vậy (√y – 2)2 = - ⇔ (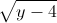
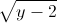)2 = - 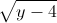= 0 ⇔ y = 4 (nhận)
Vậy giá trị y cần tìm là y = 4.
A√y = 2√y – 3 –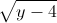
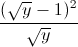⇔ √y = 6√y – 3 –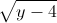
(√y)2 - 2√y + 1 - 2√y + 3 = -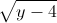
(√y)2 - 4√y + 4 = -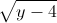
(√y – 2)2 = -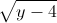
Ta có (√y – 2)2 ≥ 0 với ∀y ∈ TXĐ. Dấu “=” xảy ra khi √y – 2 = 0 ⇔ y = 4
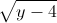- ≤ 0 với ∀y ∈ TXĐ. Dấu “=” xảy ra khi y – 4 = 0 ⇔ y = 4.
Vậy (√y – 2)2 = - 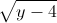⇔ (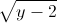)2 = - 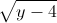= 0 ⇔ y = 4 (nhận)
Vậy giá trị y cần tìm là y = 4.
Câu hỏi liên quan
-
Cho hệ phương trình:
Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-
Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-
Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-
Chứng minh DM.CE=DE.CM
-
Giải hệ phương trình
-
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Giải phương trình (1) khi m = -5
-
Rút gọn biểu thức A
-
Tìm b để A =
-
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm