Skip to main content
/ Luyện Thi Vào Lớp 10 Môn Toán / Câu hỏi 53704

Tìm điều kiện của a và b để M xác định và rút gọn M

Tìm điều kiện của a và b để M xác định và rút gọn M

Câu hỏi

Nhận biết

Tìm điều kiện của a và b để M xác định và rút gọn M


A.
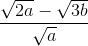
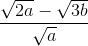
a > 0 và b ≥ 0 ; M = \frac{\sqrt{2a}-\sqrt{3b}}{\sqrt{a}}
B.
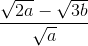
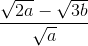
a < 0 và b ≥ 0 ; M = \frac{\sqrt{2a}-\sqrt{3b}}{\sqrt{a}}
C.
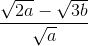
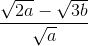
a > 0 và b < 0 ; M = \frac{\sqrt{2a}-\sqrt{3b}}{\sqrt{a}}
D.
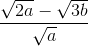
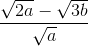
a < 0 và b < 0 ; M = \frac{\sqrt{2a}-\sqrt{3b}}{\sqrt{a}}
Đáp án đúng: A

Lời giải của Luyện Tập 365

ĐKXĐ : a, b ≥ 0 và a ≠ 0 ⇔ a > 0 và b ≥ 0

M = 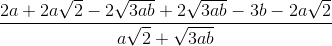\frac{2a+2a\sqrt{2}-2\sqrt{3ab}+2\sqrt{3ab}-3b-2a\sqrt{2}}{a\sqrt{2}+\sqrt{3ab}}

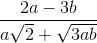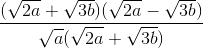
= \frac{2a-3b}{a\sqrt{2}+\sqrt{3ab}} = \frac{(\sqrt{2a}+\sqrt{3b})(\sqrt{2a}-\sqrt{3b})}{\sqrt{a}(\sqrt{2a}+\sqrt{3b})} 

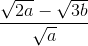
= \frac{\sqrt{2a}-\sqrt{3b}}{\sqrt{a}}

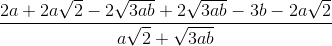
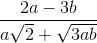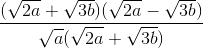
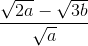
Câu hỏi liên quan

  • Giải phương trình (1) khi m = -5

    Giải phương trình (1) khi m = -5

    Chi tiết
  • Rút gọn biểu thức A

    Rút gọn biểu thức A

    Chi tiết
  • AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.

    AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.

    Chi tiết
  • Rút gọn A

    Rút gọn A

    Chi tiết
  • Tính giá trị biểu thức của A với x =

    Tính giá trị biểu thức của A với x = frac{1}{2}

    Chi tiết
  • Tìm b để A =

    Tìm b để A = frac{5}{2}

    Chi tiết
  • Tính AC và BD biết

    Tính AC và BD biết widehat{AOC} = alpha. Chứng tỏ tích AC.BD không phụ thuộc vào  alpha

    Chi tiết
  • Cho phương trình x2- 4x + m = 0 (1), với m là tham số.

    Cho phương trình x2- 4x + m = 0 (1), với m là tham số.

    Trả lời câu hỏi dưới đây:

    Giải phương trình (1) khi m = -5

    Chi tiết
  • Cho phương trình: ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)

    Cho phương trình: 

    ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)

    Trả lời câu hỏi dưới đây:

    Giải phương trình với a = -2

    Chi tiết
  • Chứng minh DM.CE=DE.CM

    Chứng minh DM.CE=DE.CM

    Chi tiết