Số đo cung nhỏ của (O) lớn hơn số đo cung nhỏ của (O').
Câu hỏi
Nhận biếtSố đo cung nhỏ của (O) lớn hơn số đo cung nhỏ của (O').
Đáp án đúng: A
Lời giải của Luyện Tập 365
Gọi các giao điểm của (O) với (O') là A, B. Nếu O và O' nằm trên cùng một nửa mặt phẳng bờ AB, ta có thể thay thế (O; R) bằng (O1, R) đối xứng với (O; R) qua AB nên chỉ cần xét trường hợp (O), (O') nằm trên hai nửa mặt phẳng bờ AB đối nhau. Vì số đo cung nhỏ AB của (O) lớn hơn nên góc ở tâm AOB lớn hơn.
Như thế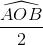 
> 
= 
.
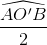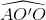Từ đó , ta có trong ∆ AO'O :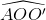 
> 90° > 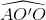do đó AO' > AO, hay
R' > R.
Gọi các giao điểm của (O) với (O') là A, B. Nếu O và O' nằm trên cùng một nửa mặt phẳng bờ AB, ta có thể thay thế (O; R) bằng (O1, R) đối xứng với (O; R) qua AB nên chỉ cần xét trường hợp (O), (O') nằm trên hai nửa mặt phẳng bờ AB đối nhau. Vì số đo cung nhỏ AB của (O) lớn hơn nên góc ở tâm AOB lớn hơn.
Như thế > = .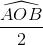
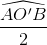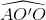Từ đó , ta có trong ∆ AO'O : > 90° > do đó AO' > AO, hay
R' > R.
Câu hỏi liên quan
-
Rút gọn A
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-
Giải hệ phương trình với a = 2
-
AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-
Tìm b để A =
-
Giải phương trình (1) khi m = -5
-
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0