Sau khi đổ đầy vào dầu nhánh B, người ta thả nhẹ nhàng một vật hình trụ đặc, đồng chất tiết diện S3 = 60cm3, cao h3 = 10cm, khối lượng riêng D3 = 600kg/m3 vào nhánh A. Hãy tính khối lượng dầu tràn ra ngoài.
Câu hỏi
Nhận biếtSau khi đổ đầy vào dầu nhánh B, người ta thả nhẹ nhàng một vật hình trụ đặc, đồng chất tiết diện S3 = 60cm3, cao h3 = 10cm, khối lượng riêng D3 = 600kg/m3 vào nhánh A. Hãy tính khối lượng dầu tràn ra ngoài.
Đáp án đúng: D
Lời giải của Luyện Tập 365
Khi khối trụ cân bằng nước dâng lên ở các nhánh A, B lần lượt là a, b
Với :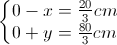 
Gọi thể tích chiếm chỗ của khối trụ trong nước là V1.
Do D3 < D1 nên khối trụ nổi trên nước. FA = P3.
Tức là : V1d1 = V3d3 => V1 = 360cm3
Mặt khác V1 = a.S1+ b.S2 = a + 2b = 3,6 (3)
Gọi C, D là hai điểm cùng nằm ngang với mặt phẳng phân cách giữa dầu và nước A và B sau khi thả khối trụ (hình vẽ 4).
=> PC = PD
=> (x + y – b + a)d1 = (h + y –b)d2
=>(x + y)d1 + (a – b)d1 = (h + y)d2 – b.d2.
Theo câu 1 : (x + y)d1 = (h + y)d2
=> a = b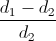 
=> b = 4a (4)
Từ (3) và (4) a = 0,4cm, b = 1,6cm thỏa mãn với điều kiện trên. Vậy thể tích đã tràn ra khỏi bình B là : ∆V = b.S2 = 0,32.10-3m3
Khối lượng dầu tràn ra ngoài là : ∆m = ∆V.D2 = 0,24kg.
Khi khối trụ cân bằng nước dâng lên ở các nhánh A, B lần lượt là a, b
Với :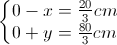
Gọi thể tích chiếm chỗ của khối trụ trong nước là V1.
Do D3 < D1 nên khối trụ nổi trên nước. FA = P3.
Tức là : V1d1 = V3d3 => V1 = 360cm3
Mặt khác V1 = a.S1+ b.S2 = a + 2b = 3,6 (3)
Gọi C, D là hai điểm cùng nằm ngang với mặt phẳng phân cách giữa dầu và nước A và B sau khi thả khối trụ (hình vẽ 4).
=> PC = PD
=> (x + y – b + a)d1 = (h + y –b)d2
=>(x + y)d1 + (a – b)d1 = (h + y)d2 – b.d2.
Theo câu 1 : (x + y)d1 = (h + y)d2
=> a = b 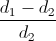=> b = 4a (4)
Từ (3) và (4) a = 0,4cm, b = 1,6cm thỏa mãn với điều kiện trên. Vậy thể tích đã tràn ra khỏi bình B là : ∆V = b.S2 = 0,32.10-3m3
Khối lượng dầu tràn ra ngoài là : ∆m = ∆V.D2 = 0,24kg.
Câu hỏi liên quan
-
Cho R3 = 6Ω. Tìm cường độ dòng điện qua các điện trở R1, R3 và số chỉ của ampe kế.
-
Pa-lăng ở câu trên được mắc theo cách khác nhưng vẫn có
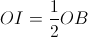(Hình 3) người đó phải tác dụng vào dây một lực F bằng bao nhiêu để tấm ván OB nằm ngang thăng bằng ? Tính lực F’ do ván tác dụng vào điểm tựa O ? (Bỏ qua ma sát ở các ròng rọc và trọng lượng của dây, của ròng rọc) -
Tính lượng nước m và nhiệt độ khi có cân bằng nhiệt trong bình 2 (t’2).
-
Điều chỉnh con chạy C sao cho phần biến trở RAC = 24Ω. Hãy tìm : - Điện trở tương đương của đoạn mạch AB. - Cường độ dòng điện qua đèn và nhiệt lượng tỏa ra trên R1 trong thời gian 10 phút.
-
Điều chỉnh con chạy C để đèn sáng bình thường, hỏi con chạy C đã chia biến trở thành hai phần có tỉ lệ như thế nào?
-
Nếu tiếp tục thực hiện như vậy một lần nữa, thì nhiệt độ cân bằng nhiệt ở mỗi bình lúc này bằng bao nhiêu?
-
Sau thấu kính L1 người ta đặt một thấu kính phân kì L2 có tiêu cự f2 = . Thấu kính L2 cách thấu kính L1 một khoảng O1O2 = , trục chính của thấu kính trùng nhau (Hình vẽ 3). Vẽ ảnh của vật AB qua hai thấu kính trên và dùng hình học ( không dùng công thức thấu kính) tìm khoảng cách từ ảnh cuối cùng A2B2 đến thấu kính phân kỳ.
-
Cho U = 16V, R = 8Ω, k = 3, xác định Rx để công suất trên Rx bằng 0,4W.
-
Tìm độ cao của cột nước cần đổ vào chậu (tính từ đáy đến mặt thoáng) biết khối lượng riêng của thanh AB và của nước lần lượt là : Dt = 1120 kg/m3 và Dn = 1000 kg/m3?
-
Thấu kính trên là thấu kính gì (HS tự giải)? Vẽ hình (HS tự giải) . Tính tiêu cự của thấu kính và độ lớn của các ảnh theo h; d1 và d2.