Một vật dao động điều hòa theo phương trình x = 5cos(2πt - π/4) cm. Tốc độ trung bình của vật trong khoảng thời gian từ t1 = 1s đến t2 = 4,625s là:

Câu hỏi
Nhận biếtMột vật dao động điều hòa theo phương trình x = 5cos(2πt - π/4) cm. Tốc độ trung bình của vật trong khoảng thời gian từ t1 = 1s đến t2 = 4,625s là:
Đáp án đúng: D
Phương pháp giải
Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn
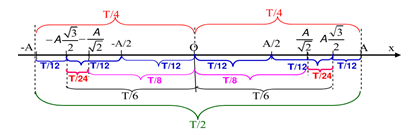
Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn
Lời giải của Luyện Tập 365
T = 2π/ω = 1 (s)
\(\eqalign{ & \Delta t = \left| {{t_2} - {t_1}} \right| = 3,625{\rm{s}} \cr & \to {{\Delta t} \over T} = 3,625 \to \Delta t = 3,625T = 3T + {{5T} \over 8} \cr} \)
Ta có: \(\Delta t = 3,625 = 3T + {T \over 2} + {T \over 8}\)
theo hình vẽ :\(\Delta t = 3T + {5T \over 8} = 3T + {T \over 4} + {T \over 4} + {T \over 8}\)
\(S = 3.4A + 2A + A - A{{\sqrt 2 } \over 2} = 15A - A{{\sqrt 2 } \over 2} \Rightarrow {v_{tb}} = {S \over {\Delta t}} = {{15A - A{{\sqrt 2 } \over 2}} \over {3,625}} \approx 19,71cm/s\)
T = 2π/ω = 1 (s)
\(\eqalign{ & \Delta t = \left| {{t_2} - {t_1}} \right| = 3,625{\rm{s}} \cr & \to {{\Delta t} \over T} = 3,625 \to \Delta t = 3,625T = 3T + {{5T} \over 8} \cr} \)
Ta có: \(\Delta t = 3,625 = 3T + {T \over 2} + {T \over 8}\)
theo hình vẽ :\(\Delta t = 3T + {5T \over 8} = 3T + {T \over 4} + {T \over 4} + {T \over 8}\)
\(S = 3.4A + 2A + A - A{{\sqrt 2 } \over 2} = 15A - A{{\sqrt 2 } \over 2} \Rightarrow {v_{tb}} = {S \over {\Delta t}} = {{15A - A{{\sqrt 2 } \over 2}} \over {3,625}} \approx 19,71cm/s\)
Câu hỏi liên quan
-

Dao động cơ học là
-

Trong chương trình của vật dao động điều hòa x = Acos(ωt + φ), radian trên giây (rad/s) là đơn vị của đại lượng nào sau đây:
-

Dao động của một vật có phương trình: x = acosωt + asinωt. Biên độ dao động của vật là
-

Khi chiếu hai tia sáng đơn sắc song song màu đỏ và màu lục từ không khí vào lăng kính thủy tinh và có tia ló thì:
-

Ánh sáng đơn sắc là ánh sáng:
-

Một vật nhỏ dao động điều hòa theo một trục cố định. Phát biểu nào sau đây đúng?
-

Biên độ của vật dao động điều hòa phụ thuộc vào
-

Ánh sáng có tần số lớn nhất trong số các ánh sáng đơn sắc: đỏ, lam, chàm, tím là ánh sáng:
-

Chọn câu đúng
-

Một chất điểm dao động điều hòa trên trục Ox. Điểm M nằm trên trục Ox và trong quá trình dao động chất điểm không đi qua M. Tại thời điểm t1 chất điểm ở xa M nhất; tại thời điểm t2 chất điểm ở gần M nhất thì:
