Một điểm M nằm trên một nửa đường tròn có đường kính AB cố định. Trên tia đối của tia MA lấy một điểm H sao cho MH = MB. Trả lời câu hỏi dưới đây:Gọi chung điểm của BH là K. Chứng minh rằng đường thẳng KM luôn luôn đi qua một điểm cố định.
Câu hỏi
Nhận biếtMột điểm M nằm trên một nửa đường tròn có đường kính AB cố định. Trên tia đối của tia MA lấy một điểm H sao cho MH = MB.
Trả lời câu hỏi dưới đây:
Gọi chung điểm của BH là K. Chứng minh rằng đường thẳng KM luôn luôn đi qua một điểm cố định.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Xét giao điểm P của MK với cung AB. Vì tam giác MHB cân đỉnh M nên MK vừa là trung tuyến (do KB = KH) vừa là phân giác, do đó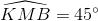 
.
Ta cósđ cung PB =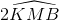 
= 90°
Vậy P là điểm chính giữa cung AB và do đó cố định (P chính là tâm của cung (
) vì PH1 = PB = PA).
Xét giao điểm P của MK với cung AB. Vì tam giác MHB cân đỉnh M nên MK vừa là trung tuyến (do KB = KH) vừa là phân giác, do đó .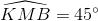
Ta cósđ cung PB = = 90°
Vậy P là điểm chính giữa cung AB và do đó cố định (P chính là tâm của cung (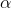) vì PH1 = PB = PA).
Câu hỏi liên quan
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Tính giá trị biểu thức của A với x =
-
Giải hệ phương trình với a = 2
-
Tìm a để phương trình có 2 nghiệm nguyên
-
Tìm b để A =
-
Tính AC và BD biết
= 
. Chứng tỏ tích AC.BD không phụ thuộc vào -
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-
Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-
Cho hệ phương trình:
Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2