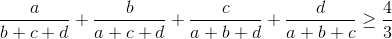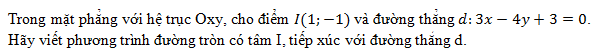Khảo sát tính đơn điệu của các hàm số sau:
1) y = f(x) = 2x + 3
2) y = f(x) = ![sqrt[3]{x}](https://luyentap365.com/wp-content/picture/learning/exam/2015/0828/106048_441029_1.gif) 3) y = f(x) =
3) y = f(x) = 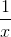 4) y = f(x) =
4) y = f(x) = 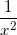

Câu hỏi
Nhận biếtKhảo sát tính đơn điệu của các hàm số sau:
1) y = f(x) = 2x + 3
2) y = f(x) = ![sqrt[3]{x}](https://luyentap365.com/wp-content/picture/learning/exam/2015/0828/106048_441029_1.gif)
3) y = f(x) = 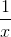
4) y = f(x) = 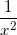
2) Hàm giảm trên R
3) Hàm giảm trên R
4) Hàm giảm trên (0;+∞) và tăng trên (-∞; 0)
2) Hàm tăng trên R
3) Hàm giảm trên R
4) Hàm tăng trên R
2) Hàm tăng trên R
3) Hàm giảm trên R
4) Hàm giảm trên R
2) Hàm tăng trên R
3) Hàm giảm trên R
4) Hàm giảm trên (0;+∞) và tăng trên (-∞; 0)
Đáp án đúng: D
Lời giải của Luyện Tập 365
1)
Miền xác định D = R
Giả sử 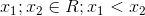
Ta xét : 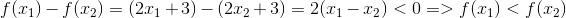
=> Hàm tăng trên R
2)
Miền xác định D = R
Giả sử 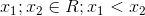
Ta xét :
![f(x_{1})-f(x_{2})=sqrt[3]{x_{1}}-sqrt[3]{x_{2}}<0 =>f(x_{1})<f(x_{2})](https://luyentap365.com/wp-content/picture/learning/exam/2015/0828/v99195_265628_4.gif)
=> Hàm tăng trên R
3) Hàm có miền xác định D = R {0}
+) Giả sử
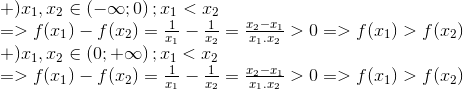
=> Hàm giảm trên R
4) Hàm có miền xác định D = R {0}
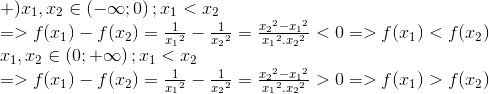
1)
Miền xác định D = R
Giả sử 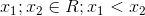
Ta xét : 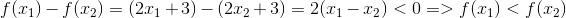
=> Hàm tăng trên R
2)
Miền xác định D = R
Giả sử 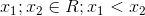
Ta xét :
![f(x_{1})-f(x_{2})=sqrt[3]{x_{1}}-sqrt[3]{x_{2}}<0 =>f(x_{1})<f(x_{2})](https://luyentap365.com/wp-content/picture/learning/exam/2015/0828/v99195_265628_4.gif)
=> Hàm tăng trên R
3) Hàm có miền xác định D = R {0}
+) Giả sử
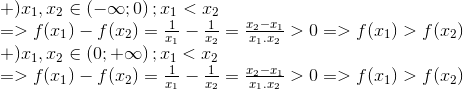
=> Hàm giảm trên R
4) Hàm có miền xác định D = R {0}
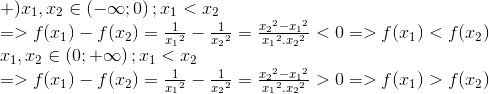
Câu hỏi liên quan
-

. Cho tam giác ABC với A(-1;2);B(-2;5);C(0;-3).
a) Tính tọa độ trọng tâm G của tam giác ABC.
b) Tìm tọa độ điểm D sao cho tứ giác ADBC là hình bình hành
-

Xác định hàm số bậc hai
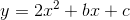 biết rằng đồ thị của nó có hoành độ đỉnh là 2 và đị qua điểm M(1;-2)
biết rằng đồ thị của nó có hoành độ đỉnh là 2 và đị qua điểm M(1;-2) -

Xác định hàm số bậc hai
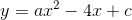 biết rằng đồ thị của nó cắt Oy tại điểm có tung độ -3 và đi qua điểm M(-2;1).
biết rằng đồ thị của nó cắt Oy tại điểm có tung độ -3 và đi qua điểm M(-2;1). -

-

cơ bản

-

Dùng định nghĩa để tìm khoảng tăng giảm của hàm số:
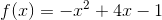
-

Dùng định nghĩa để tìm khảng tăng giảm của hàm số
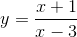
-

Tìm tập xác định của các hàm số sau:
a)
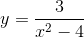
b)
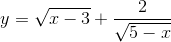
c)
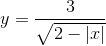
-

-

Cho a, b, c, d là các số thực dương. Chứng minh rằng: