Skip to main content
/ Luyện Thi Vào Lớp 10 Môn Toán / Câu hỏi 53300

Hai vòi nước cung chảy vào một bể không có nước thì trong 6 giờ đày bể. Nếu vòi thứ nhất chảy trong 2 giờ, vòi thứ hai chảy trong 3 giờ thì được  \frac{2}{5} bể. Hỏi mỗi vòi chảy một mình thì trong bao lâu sẽ đầy bể?

Hai vòi nước cung chảy vào một bể không có nước thì trong 6 giờ đày bể. Nếu vòi thứ nhất

Câu hỏi

Nhận biết

Hai vòi nước cung chảy vào một bể không có nước thì trong 6 giờ đày bể. Nếu vòi thứ nhất chảy trong 2 giờ, vòi thứ hai chảy trong 3 giờ thì được  \frac{2}{5} bể. Hỏi mỗi vòi chảy một mình thì trong bao lâu sẽ đầy bể?


A.
Vòi thứ nhất chảy một mình mất 10 giờ, vòi thứ hai chạy một mình hết 15 giờ.
B.
Vòi thứ nhất chảy một mình mất 15 giờ, vòi thứ hai chạy một mình hết 10 giờ.
C.
vòi thứ nhất chảy một mình mất 14 giờ, vòi thứ hai chạy một mình hết 15 giờ.
D.
vòi thứ nhất chảy một mình mất 15 giờ, vòi thứ hai chạy một mình hết 14 giờ.
Đáp án đúng: A

Lời giải của Luyện Tập 365

Gọi x, y lần lượt là số giờ vòi thứ nhất và thứ hai chảy một mình đầy bể

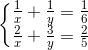
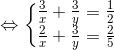
Ta có hệ phương trình sau: \left\{\begin{matrix} \frac{1}{x}+\frac{1}{y}=\frac{1}{6}\\ \frac{2}{x}+\frac{3}{y}=\frac{2}{5} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{3}{x}+\frac{3}{y}=\frac{1}{2}\\ \frac{2}{x}+\frac{3}{y}=\frac{2}{5} \end{matrix}\right.

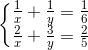
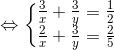
Giải hệ phương trình ta tìm được nghiệm: x = 10 và y = 15

Kết luận: x = 10 và y = 15 thỏa mãn điều kiện của bài toán. Vậy vòi thứ nhất chảy một mình mất 10 giờ, vòi thứ hai chạy một mình hết 15 giờ.

Câu hỏi liên quan

  • Cho phương trình x2- 4x + m = 0 (1), với m là tham số.

    Cho phương trình x2- 4x + m = 0 (1), với m là tham số.

    Trả lời câu hỏi dưới đây:

    Giải phương trình (1) khi m = -5

    Chi tiết
  • Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2  

    Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn:  x2  - 12x – 14y < 0 

    Chi tiết
  • Tính giá trị biểu thức của A với x =

    Tính giá trị biểu thức của A với x = frac{1}{2}

    Chi tiết
  • Cho nửa đường tròn (O), đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E khắc

    Cho nửa đường tròn (O), đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E khắc với điểm A. Từ các điểm E, A và B kẻ các tiếp tuyến của nửa đường tròn (O). Tiếp tuyến kẻ từ E lần lượt cắt các tiếp tuyến từ điểm A và B tại C và D.

    Trả lời câu hỏi dưới đây:

    Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.

    Chi tiết
  • Giải phương trình với a = -2

    Giải phương trình với a = -2

    Chi tiết
  • Tìm b để A =

    Tìm b để A = frac{5}{2}

    Chi tiết
  • Chứng minh rằng: AM2 = AN.AB

    Chứng minh rằng: AM2 = AN.AB

    Chi tiết
  • Cho Parabol  (P): ax2(a ≠ 0) và đường thẳng d: y=2x

    Cho Parabol  (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.

    Chi tiết
  • Cho biểu thức:A =

    Cho biểu thức:

    A = left ( frac{3}{sqrt{b}-1}+frac{sqrt{b}-3}{b-1} right ):left ( frac{b+2}{b+sqrt{b}-2}-frac{sqrt{b}}{sqrt{b}+2} right )

    Trả lời câu hỏi dưới đây:

    Rút gọn A

    Chi tiết
  • Rút gọn A

    Rút gọn A

    Chi tiết