Hai vận động viên chạy với vận tốc đều theo một đường vòng khép kín trong sân vận động . Người thứ nhất chạy hết một vòng ít thời gian hơn người thứ hai 5 giây. Nếu hai người cùng xuất phát tại một điểm và chạy cùng chiều thì sau 30 giây người thứ nhất lại đuổi kịp người thứ hai. Sau thời gian bao lâu họ sẽ gặp nhau nếu cả hai cùng xuất phát từ một điểm và chạy ngược chiều nhau.
Câu hỏi
Nhận biếtHai vận động viên chạy với vận tốc đều theo một đường vòng khép kín trong sân vận động . Người thứ nhất chạy hết một vòng ít thời gian hơn người thứ hai 5 giây. Nếu hai người cùng xuất phát tại một điểm và chạy cùng chiều thì sau 30 giây người thứ nhất lại đuổi kịp người thứ hai. Sau thời gian bao lâu họ sẽ gặp nhau nếu cả hai cùng xuất phát từ một điểm và chạy ngược chiều nhau.
Đáp án đúng: B
Lời giải của Luyện Tập 365
Gọi v1, v2 theo thứ tự là vận tốc của người thứ nhất và người thứ hai (đơn vị m/s) và v1 > v2 > 0) và quãng đường trong một vòng là S (m).
Theo điều kiện đề bài ta có phương trình:
<=> 
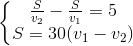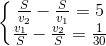
Đặt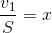 
; 
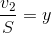ta có:
\\&space;x-y=\frac{1}{30}&space;\:&space;\:&space;\:&space;\:&space;\:&space;\:&space;(2)&space;\end{matrix}\right.)
<=> &space;\\&space;x=\frac{1}{30}+y\:&space;\:&space;\:&space;(2)\end{matrix}\right.)
(1) <=> 150y2 + 5y – 1 = 0 <=>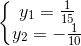 
y2 < 0 (loại)
=> 
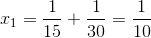
Gọi t là thời gian để hai người chạy ngược chiều gặp nhau, ta có:
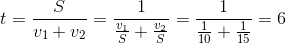
Vậy thời gian để họ gặp nhau là 6 giây.
Gọi v1, v2 theo thứ tự là vận tốc của người thứ nhất và người thứ hai (đơn vị m/s) và v1 > v2 > 0) và quãng đường trong một vòng là S (m).
Theo điều kiện đề bài ta có phương trình:
<=>
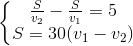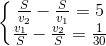
Đặt 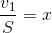; 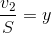ta có:
<=>
(1) <=> 150y2 + 5y – 1 = 0 <=>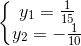
y2 < 0 (loại)
=>
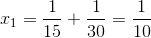
Gọi t là thời gian để hai người chạy ngược chiều gặp nhau, ta có:
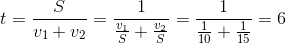
Vậy thời gian để họ gặp nhau là 6 giây.
Câu hỏi liên quan
-
Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-
AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-
Tìm m để phương trình (1) có nghiệm .
-
Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-
Giải hệ phương trình
